等比数列とは
等比数列 … 初項に一定の数をかけて得られる数列
かけていく一定の数のことを 公比 といい,$r$ で表す
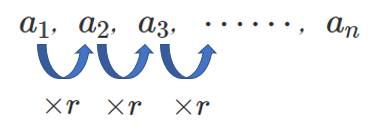
等差数列の例
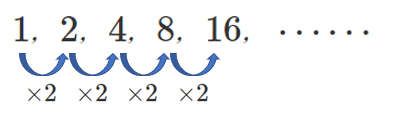
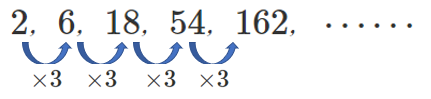
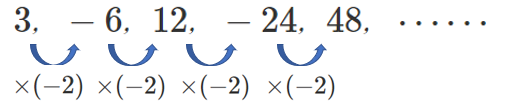
等比数列の一般項
初項 $a$,公比 $r$ の等比数列 $\{a_n\}$
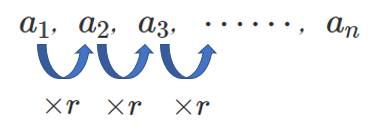
第 $2$ 項は初項に公比を $1$ 回かけると求まる
第 $3$ 項は初項に公比を $2$ 回かけると求まる
第 $4$ 項は初項に公比を $3$ 回かけると求まる
これより
第 $n$ 項は 初項に公比を $(n-1)$ 回かけると求まる
初項 $a$,公比 $r$ の等比数列 $\{a_n\}$ の一般項は
$a_n=ar^{n-1}$

一般項を求めてみよう!
次のような等比数列の一般項を求めよ。
(1) 初項 $2$,公比 $3$
(2) 初項 $-2$,公比 $-3$
(3) 初項 $3$,公比 $3$
(4) 初項 $1$,公比 $\displaystyle{\frac{1}{2}}$
(1) 初項 $2$,公比 $3$
$a_n=2\cdot3^{n-1}$
(2) 初項 $-2$,公比 $-3$
$a_n=-2(-3)^{n-1}$
(3) 初項 $3$,公比 $3$
$a_n=3\cdot3^{n-1}=3^n$
(4) 初項 $1$,公比 $\displaystyle{\frac{1}{2}}$
$\displaystyle{a_n=\left(\frac{1}{2}\right)^{n-1}}$

初項が $1$,公比 $-2$ の等比数列の一般項 $a_n$ を求めてみよう!

$a_n=(-2)^{n-1}$ かな?
かっこは外せるの?

かっこは外せないことを知っておこう!
よく間違えるので注意!
<かっこが外せない理由>
$(-2)^{n-1}$ と $-2^{n-1}$ は異なる文字式
$n=3$ を代入してみると
$(-2)^{n-1}$ は $(-2)^2=4$($(-2)$ を $2$ 回かける)
$-2^{n-1}$ は $-2^2=-4$($2$ を $2$ 回かけてマイナスをつける)
同じ数を代入して異なる数になるので,$(-2)^{n-1}$ と $-2^{n-1}$ は異なる文字式
問題

等比数列の一般項に関する問題を解いてみよう!
初項 $a$,公比 $r$ とすると
$a_n=ar^{n-1}$
$a_4=24$ より
$ar^3=24$ $\cdots\cdots$ ①
$a_6=96$ より
$ar^5=96$ $\cdots\cdots$ ②
②について
$(ar^3)\cdot r^2=96$
①を代入すると
$24r^2=96$
$r^2=4$
$r=±2$
$r=2$ のとき,$a=3$
$r=-2$ のとき,$a=-3$
したがって
$a_n=3\cdot2^{n-1}$ または $a_n=-3(-2)^{n-1}$
まとめ
● 等比数列の一般項
初項 $a$,公比 $r$ の等差数列 $\{a_n\}$ の一般項は
$a_n=ar^{n-1}$

等差数列とごちゃごちゃにならないようにしよう!




コメント