漸化式とは
漸化式 … 前の項から次の項を求めるための関係式
数列において,初項と隣り合う $2$ 項間の関係(漸化式)が分かれば,すべての項が定まる
例えば
\begin{eqnarray} &[1]& a_1=1 \\\\ &[2]& a_{n+1}=2a_n (n=1,2,3,\cdots\cdots) \end{eqnarray}$[2]$ の式に $n=1$ を代入すると
$a_2=2a_1=2\cdot1=2$
$[2]$ の式に $n=2$ を代入すると
$a_3=2a_2=2\cdot2=4$
$[2]$ の式に $n=3$ を代入すると
$a_4=2a_3=2\cdot4=8$
というように,漸化式により前後の関係が分かれば,初項から次の項を順に求めることができる
漸化式の基本パターン

初項と漸化式が与えられた場合に一般項を求めてみよう!
以下の4パターンは確実に求められるように練習しよう!
① $a_{n+1}=a_n+d$
② $a_{n+1}=ra_n$
③ $a_{n+1}=a_n+(nの式)$
④ $a_{n+1}=pa_n+q$

漸化式の形を見たら解き方が分かるようにしよう!
① $a_{n+1}=a_n+d$
$n=1$ を代入すると
$a_2=a_1+3=2+3=5$
$n=2$ を代入すると
$a_3=a_2+3=5+3=8$
$n=3$ を代入すると
$a_4=a_3+3=8+3=11$
数列 $\{a_n\}$ を並べてみると
$2,5,8,11,\cdots\cdots$
数列 $\{a_n\}$ は初項 $2$,公差 $3$ の等差数列であることがわかる
$a_{n+1}=a_n+3$ が表しているのは
前の項に $3$ を足すと次の項が求まる
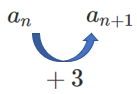
ということ
以上より,数列 $\{a_n\}$ の漸化式が $a_{n+1}=a_n+d$ で表されるとき
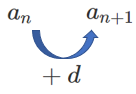
数列 $\{a_n\}$ は公差 $d$ の等差数列である

初項 $a$,公差 $d$ の等差数列 $\{a_n\}$ の一般項は覚えてる?

$a_n=a+(n-1)d$ だったよね!
等差数列の一般項についてはこれ↓

次の条件によって定められる数列 $\{a_n\}$ の一般項を求めよ。
(1) $a_1=1$,$a_{n+1}=a_n+4$
(2) $a_1=5$,$a_{n+1}=a_n-3$
(1) $a_1=1$,$a_{n+1}=a_n+4$
数列 $\{a_n\}$ は初項 $1$,公差 $4$ の等差数列であるので
$a_n=1+(n-1)\cdot4=4n-3$
(2) $a_1=5$,$a_{n+1}=a_n-3$
数列 $\{a_n\}$ は初項 $5$,公差 $-3$ の等差数列であるので
$a_n=5+(n-1)\cdot(-3)=-3n+2$
② $a_{n+1}=ra_n$
$n=1$ を代入すると
$a_2=3a_1=3\cdot2=6$
$n=2$ を代入すると
$a_3=3a_2=3\cdot6=18$
$n=3$ を代入すると
$a_4=3a_3=3\cdot18=54$
数列 $\{a_n\}$ を並べてみると
$2,6,18,54,\cdots\cdots$
数列 $\{a_n\}$ は初項 $2$,公比 $3$ の等差数列であることがわかる
$a_{n+1}=3a_n$ が表しているのは
前の項に $3$ をかけると次の項が求まる
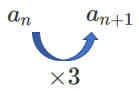
ということ
以上より,数列 $\{a_n\}$ の漸化式が $a_{n+1}=ra_n$ で表されるとき
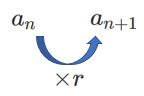
数列 $\{a_n\}$ は公比 $r$ の等差数列である

初項 $a$,公比 $d$ の等比数列 $\{a_n\}$ の一般項は覚えてる?

$a_n=ar^{n-1}$ だったよね!
等比数列の一般項についてはこれ↓

次の条件によって定められる数列 $\{a_n\}$ の一般項を求めよ。
(1) $a_1=1$,$a_{n+1}=4a_n$
(2) $a_1=5$,$a_{n+1}=-3a_n$
(1) $a_1=1$,$a_{n+1}=4a_n$
数列 $\{a_n\}$ は初項 $1$,公比 $4$ の等差数列であるので
$a_n=1\cdot4^{n-1}=4^{n-1}$
(2) $a_1=5$,$a_{n+1}=-3a_n$
数列 $\{a_n\}$ は初項 $5$,公比 $-3$ の等差数列であるので
$a_n=5(-3)^{n-1}$
まとめ
● 漸化式とは
数列において前の項から次の項を求めるための関係式
● 漸化式の基本パターン
① $a_{n+1}=a_n+d$ 公差 $d$ の等差数列
② $a_{n+1}=ra_n$ 公比 $r$ の等比数列
③ $a_{n+1}=a_n+(nの式)$
④ $a_{n+1}=pa_n+q$

まずは,等差数列と等比数列の漸化式をマスターしよう!




コメント