ベクトルの基本

ベクトルの基本は平面のベクトルと同様!
ベクトルの基本はこれ↓

ベクトルとは
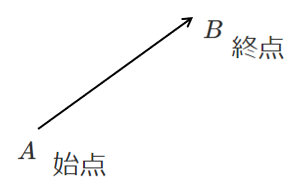
$A$ を始点,$B$ を終点とするとき,このベクトルを
$\overrightarrow{AB}$
と表す
ベクトルを $\vec{a}$,$\vec{b}$ などで表すこともある
逆ベクトル
$\vec{a}$ と大きさが等しく,向きが反対のベクトルを
$\vec{a}$ の逆ベクトル
といい
$-\vec{a}$
で表す
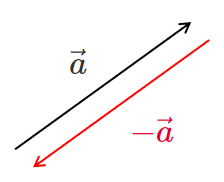
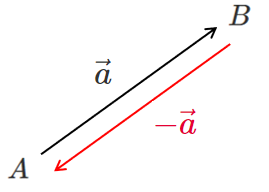
$\vec{a}=\overrightarrow{AB}$ のとき
$-\vec{a}=\overrightarrow{BA}$
すなわち
$\overrightarrow{BA}=-\overrightarrow{AB}$
等しいベクトル
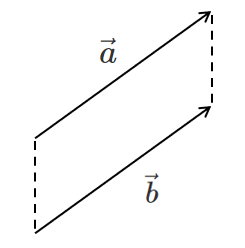
向きが同じで大きさも等しい2つのベクトル $\vec{a}$, $\vec{b}$ は等しい
といい
$\vec{a}=\vec{b}$
とかく
向きと大きさのどちらかが異なる場合は2つのベクトル $\vec{a}$, $\vec{b}$ は等しくない
向きは等しいが大きさが異なる
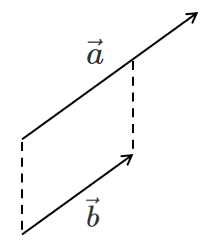
大きさは等しいが向きが異なる
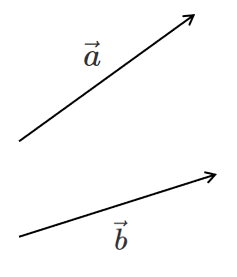
$\vec{a}≠\vec{b}$
$\vec{a}$ と $\vec{b}$ の大きさが等しい場合は
$|\vec{a}|=|\vec{b}|$
と表すことができる
問題
下の図の直方体について,次のベクトルをすべてあげよ。
(1) $\overrightarrow{AB}$ と等しいベクトル
(2) $\overrightarrow{AB}$ の逆ベクトル
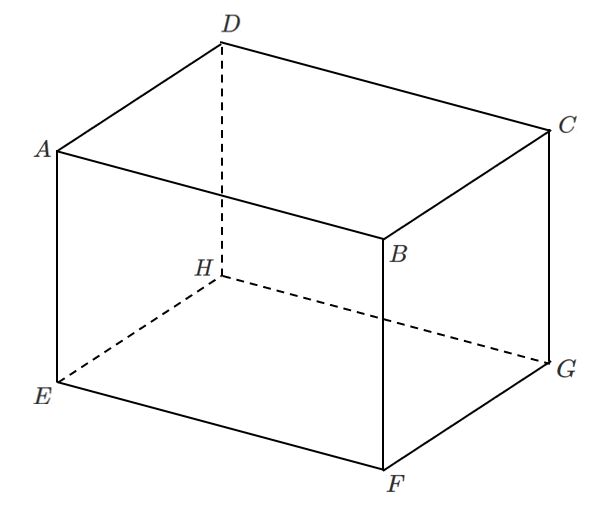
(1) $\overrightarrow{AB}$ と等しいベクトル
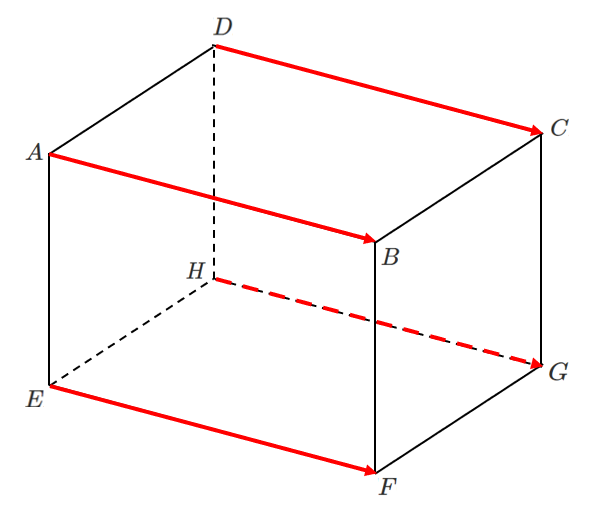
$\overrightarrow{DC}$,$\overrightarrow{EF}$,$\overrightarrow{HG}$
(2) $\overrightarrow{AB}$ の逆ベクトル
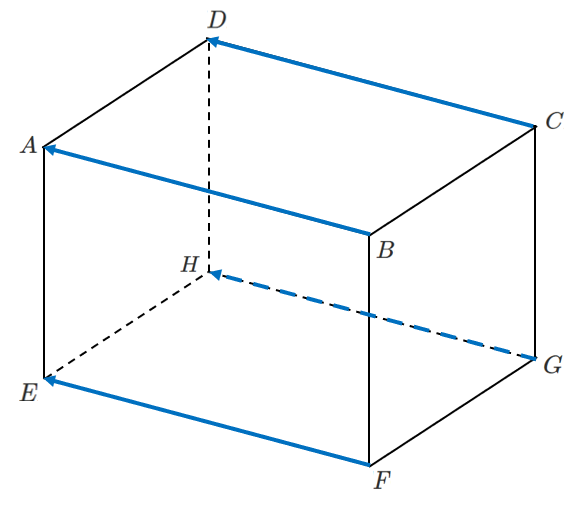
$\overrightarrow{BA}$,$\overrightarrow{CD}$,$\overrightarrow{FE}$,$\overrightarrow{GH}$
ベクトルの分解

ベクトルの加法や減法や実数倍も平面ベクトルと同様に考えることができる!
平面ベクトルで学んだ「ベクトルの分解」を用いて問題を解いてみよう!
ベクトルの分解とは
ベクトルの加法
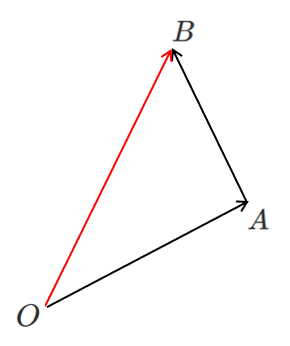
$\overrightarrow{OA}+ \overrightarrow{AB}= \overrightarrow{OB}$
を利用して
あるベクトルを和の形に分解することを「ベクトルの分解」という
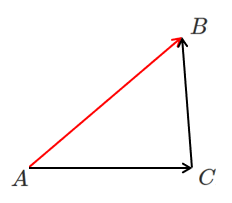
例えば,
$\overrightarrow{AB}$ について「ベクトルの分解」をすると
$\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}$
$\overrightarrow{AB}=\overrightarrow{AD}+\overrightarrow{DB}$
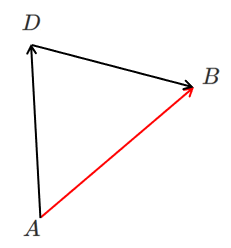
以上のように「ベクトルの分解」ができる
「ベクトルの分解」について詳しくはこれ↓

問題
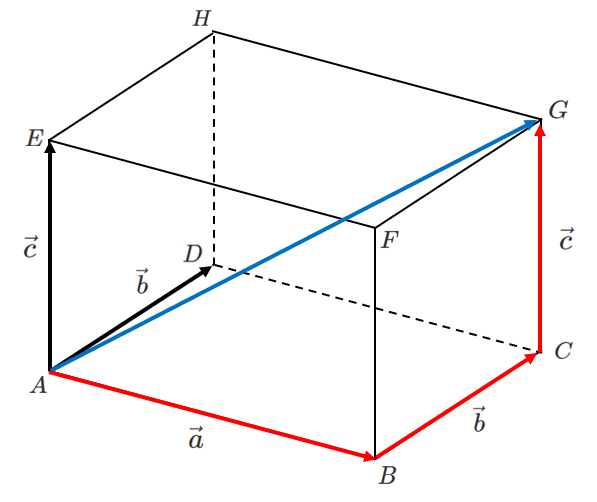
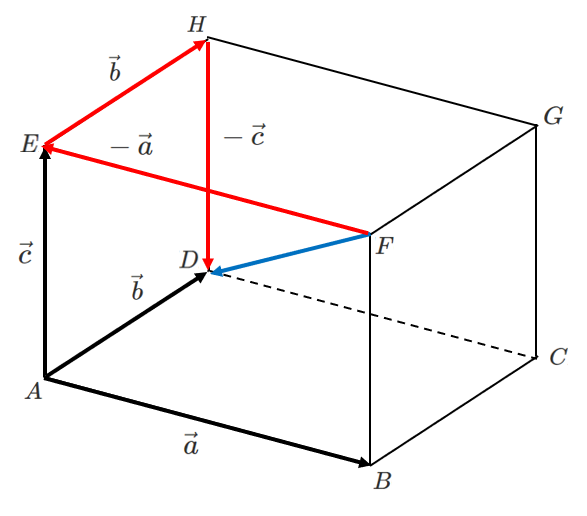
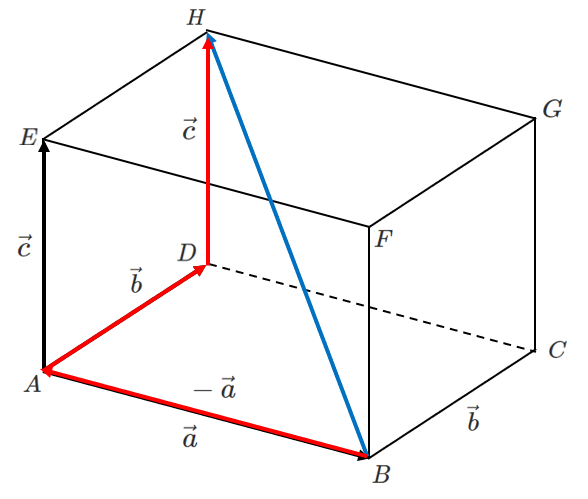
下の図の直方体において,$\overrightarrow{AB}=\vec{a}$,$\overrightarrow{AD}=\vec{b}$,$\overrightarrow{AE}=\vec{c}$ とするとき,次のベクトルを $\vec{a}$,$\vec{b}$,$\vec{c}$ を用いて表せ。
(1) $\overrightarrow{AG}$
(2) $\overrightarrow{FD}$
(3) $\overrightarrow{BH}$
(1) $\overrightarrow{AG}$
\begin{eqnarray} \overrightarrow{AG} &=& \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CG} \\\\ &=& \vec{a}+\vec{b}+\vec{c} \end{eqnarray}
(2) $\overrightarrow{FD}$
\begin{eqnarray} \overrightarrow{FD} &=& \overrightarrow{FE}+\overrightarrow{EH}+\overrightarrow{HD} \\\\ &=& -\vec{a}+\vec{b}+(-\vec{c}) \\\\ &=& -\vec{a}+\vec{b}-\vec{c} \end{eqnarray}
(3) $\overrightarrow{BH}$
\begin{eqnarray} \overrightarrow{BH} &=& \overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DH} \\\\ &=& -\vec{a}+\vec{b}+\vec{c} \end{eqnarray}

平面と同じように考えたら大丈夫だね!
まとめ
● 空間のベクトル
平面のベクトルと同様に考えることができる

新しいものを学ぶというよりは,平面ベクトルの復習と考えよう!




コメント