因数分解の最初の関門である「たすき掛け」についてわかりやすく解説します!
この投稿を見れば,数学が苦手な人でも簡単に「たすき掛け」の因数分解ができるようになります!
たすき掛けとは

「たすき掛け」ってそもそも何?

簡単に説明すると,
○$ x^2+$○$x +$○ を
$($○$ x +$○$)($○$ x +$○$)$ という形に
因数分解する方法のことを「たすき掛け」というよ!
例を下に示したよ!
たすき掛け
$3x^2+8x+4=(x+2)(3x+2)$

たすき掛けの詳しい手順を見てみよう!
たすき掛けの手順
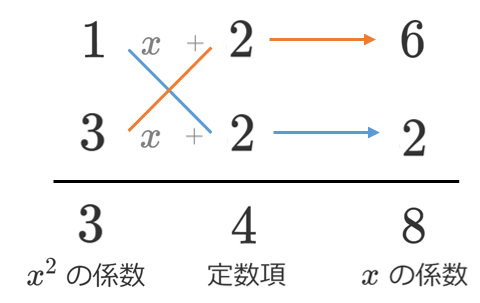
手順1 かけて $3$($x^2$ の係数)になるような $2$ つの整数を決めて縦に並べる。
かけて $3$ と言えば,$1$ と $3$ が思いつく。$-1$ と $-3$ も考えつくが,ここでは正の数同士を考えよう。

手順2 かけて $4$(定数項)になるような $2$ つの整数を決めて縦に並べる。
かけて $4$ と言えば,$1$ と $4$,$2$ と $2$,$-1$ と $-4$,$-2$ と $-2$ が思いつく。ここでは,$2$ と $2$ を選ぶ。

手順3 クロスにかけ算して,かけた結果を右に書く。
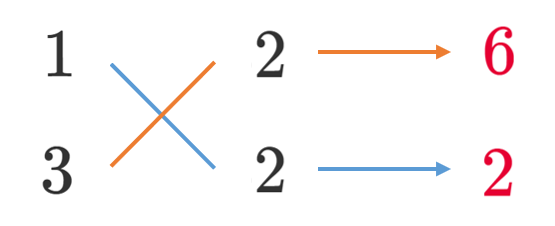
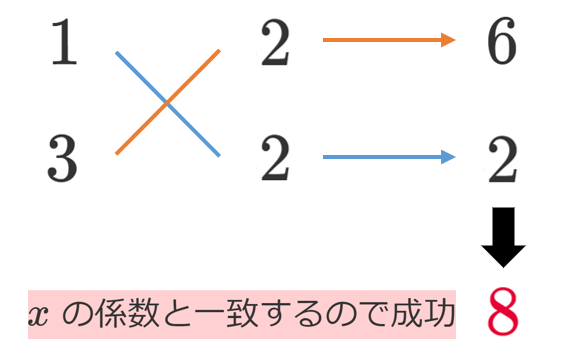
手順4 かけた結果を足し算する。足し算の結果が $x$ の係数と一致すれば,「たすき掛け」成功!
※ $x$ の係数と一致しなければ,手順1に戻ってやり直し
手順5 手順1と2で選んだ $4$ つの数を使って因数分解する。
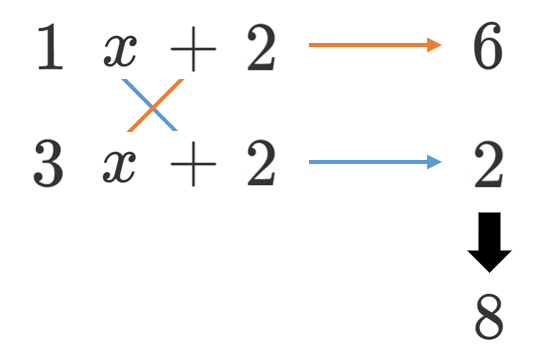
たすき掛けの練習
(1) $2x^2+7x+3$
(2) $6x^2-7x-5$
(3) $3x^2-10xy-8y^2$
(4) $ax^2-(a+2)x+2$
(1) $2x^2+7x+3=(x+3)(2x+1)$
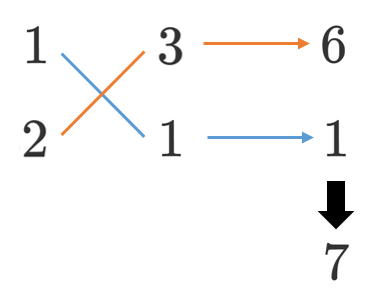
(2) $6x^2-7x-5=(2x+1)(3x-5)$
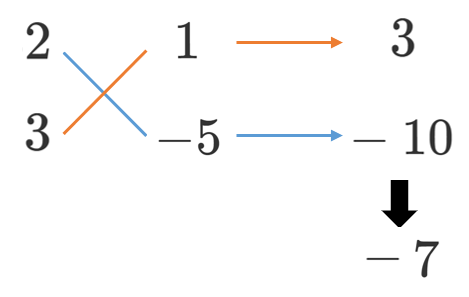
(3) $3x^2-10xy-8y^2=(3x+2y)(x-4y)$
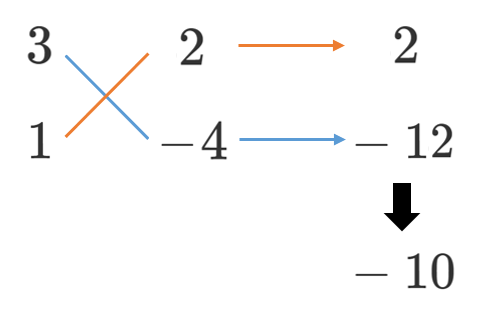
(4) $ax^2-(a+2)x+2=(x-1)(ax-2)$
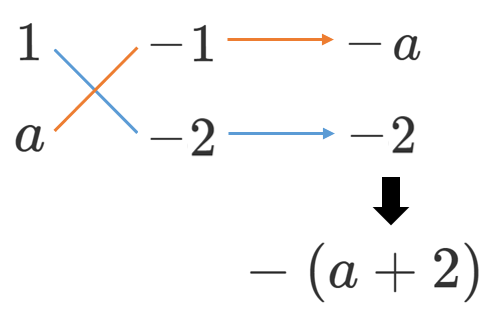
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント