2次関数のグラフの平行移動と対称移動の方法を知っていますか?
苦戦してしまう高校生が多い問題の1つです!
平行移動と対称移動のポイントは,ずばり『頂点』と『グラフの形』!
平方完成さえできれば,簡単に解けるようになります!
それに加えて,『平方完成する必要がない解法』もあります!
2次関数のみならず,3次関数などその他の関数にも応用できます!
他の受験生と差をつけたい高校生にオススメの投稿です!
この投稿であなたも『2次関数のグラフの平行移動・対称移動』をマスターできます!
2次関数の平方完成と頂点
2次関数 $y=ax^2+bx+c$ を $y=a(x-p)^2+q$ に変形することを『平方完成』という。
平方完成して,$y=a(x-p)^2+q$ の形に変形することで,軸が直線 $x=p$,頂点が $(p,q)$ であることがわかる。
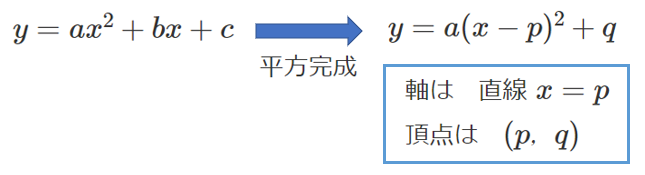
平方完成の復習はこれ↓

平行移動
頂点を利用した平行移動の方法
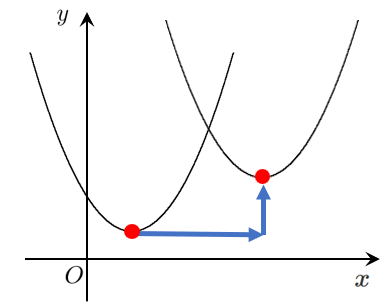
2.頂点の移動を考える
3.$x^2$ の係数($a$ の値)は変わらない

このポイントをおさえれば平行移動の問題は解ける!
(1) ①のグラフを $x$ 軸方向に $2$,$y$ 軸方向に $-1$ だけ平行移動して得られるグラフ
(2) $x$ 軸方向に $2$,$y$ 軸方向に $-1$ だけ平行移動して①のグラフと重なるようなグラフ
を求めよ。
①について $y=2(x-1)^2+2$
よって,①のグラフの頂点は $(1,2)$
(1)
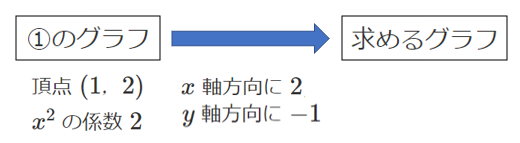
①のグラフの頂点 $(1,2)$ を
$x$ 軸方向に $2$,$y$ 軸方向に $-1$ だけ平行移動すると $(3,1)$
求めるグラフは,①のグラフを平行移動したものであるから
$x^2$ の係数は $2$ である
よって,求める方程式は $y=2(x-3)^2+1$
(2)

①のグラフの頂点 $(1,2)$ を
$x$ 軸方向に $-2$,$y$ 軸方向に $1$ だけ平行移動したものであるから
頂点は $(-1,3)$,$x^2$ の係数は $2$ である
よって,求める方程式は $y=2(x+1)^2+3$
式変形のみで平行移動する方法

平方完成して頂点を求めることなく,式変形だけで平行移動する方法を学ぼう!

平方完成が大変な2次関数でも,式変形だけで簡単にできるのは便利だね!
$y-q=f(x-p)$ すなわち $y=f(x-p)+q$

なんか難しい式だね…

もう少し簡単に表現してみるとこんな感じ!

これを使って平行移動の問題を解いてみよう!
(1) ①のグラフを $x$ 軸方向に $2$,$y$ 軸方向に $-1$ だけ平行移動して得られるグラフ
(2) $x$ 軸方向に $2$,$y$ 軸方向に $-1$ だけ平行移動して①のグラフと重なるようなグラフ
を求めよ。
(1) $y-(-1)=2(x-2)^2-4(x-2)+4$ ← $x$ を $x-2$,$y$ を $y-(-1)$
これを計算して $y=2x^2-8x+19$
(2) 求めるグラフは①のグラフを
$x$ 軸方向に $-2$,$y$ 軸方向に $1$ だけ平行移動したものであるから
$y-1=2(x+2)^2-4(x+2)+4$ ← $x$ を $x+2$,$y$ を $y-1$
これを計算して $y=2x^2+4x+5$

2次関数以外の関数にも使えるので超便利!
対称移動
頂点を利用した対称移動の方法
$x$ 軸,$y$ 軸,原点に関する対称移動は,下図のように考えられる。
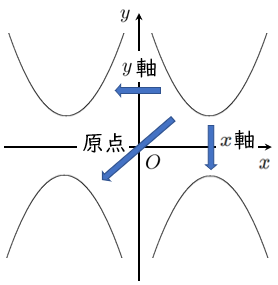
2.$x^2$ の係数($a$ の値)について
$y$ 軸に関する対称移動は符号が変わらない
$x$ 軸,原点に関する対称移動は符号が変わる
$y$ 軸に関する対称移動
1.頂点の $x$ 座標の符号が変わる
2.下に凸なら下に凸のまま,上に凸なら上に凸のまま
$x$ 軸に関する対称移動
1.頂点の $y$ 座標の符号が変わる
2.下に凸なら上に凸に,上に凸なら下に凸になる
原点に関する対称移動
1.頂点の $x$ 座標,$y$ 座標ともに符号が変わる
2.下に凸なら上に凸に,上に凸なら下に凸になる
(1) $x$ 軸に関する対称移動したグラフ
(2) $y$ 軸に関して対称移動したグラフ
(3) 原点に関して対称移動したグラフ
を求めよ。
①について $y=2(x-1)^2+2$
よって,①のグラフの頂点は $(1,2)$
(1) ①のグラフの頂点を $x$ 軸に関して対称移動すると $(1,-2)$
グラフの形は下に凸から上に凸に変わるので $y=-2(x-1)^2-2$
(2) ①のグラフの頂点を $x$ 軸に関して対称移動すると $(-1,2)$
グラフの形は変わらないので $y=2(x+1)^2+2$
(3) ①のグラフの頂点を原点に関して対称移動すると $(-1,-2)$
グラフの形は下に凸から上に凸に変わるので $y=-2(x+1)^2-2$
式変形のみで対称移動する方法

平方完成して頂点を求めることなく,式変形だけで対称移動する方法を学ぼう!

平方完成が大変な2次関数でも,式変形だけで簡単にできるのは便利だね!
曲線 $y=f(x)$ を $y$ 軸に関して対称移動した方程式は $y=f(-x)$
曲線 $y=f(x)$ を原点に関して対称移動した方程式は $y=-f(-x)$

難しい式だね…

もう少し簡単に表現するとこんな感じ!
$y$ 軸に関して対称移動したいときは $x$ を $-x$ にする
原点に関して対称移動したいときは $x$ を $-x$,$y$ を $-y$ にする

$x$ 軸に関する対称移動の場合は,$y$ 座標の符号が変わるから $y$ を $-y$ にすると考えると覚えやすい!
同様に,$y$ 軸に関する対称移動は,$x$ 座標の符号が変わるから $x$ を $-x$ にすると覚えよう!

原点に関する対称移動は,$x$ 座標も $y$ 座標も変わるから,$x$ を $-x$,$y$ を $-y$ にすると覚えればいいね!
(1) $x$ 軸に関する対称移動したグラフ
(2) $y$ 軸に関して対称移動したグラフ
(3) 原点に関して対称移動したグラフ
を求めよ。
(1) $-y=2x^2-4x+4$ ← $y$ を $-y$ にする
これを計算すると $y=-2x^2+4x-4$
(2) $y=2(-x)^2-4\cdot(-x)+4$ ← $x$ を $-x$ にする
これを計算すると $y=2x^2+4x+4$
(2) $-y=2(-x)^2-4\cdot(-x)+4$ ← $x$ を $-x$,$y$ を $-y$ にする
これを計算すると $y=-2x^2-4x-4$

2次関数以外の関数にも使えるので超便利!
まとめ
●頂点を利用した平行移動のポイント
1.問題文から移動前と移動後を整理する
2.頂点の移動を考える
3.$x^2$ の係数($a$ の値)は変わらない
●式変形のみで平行移動する方法
$x$ 軸方向に $p$,$y$ 軸方向に $q$ だけ平行移動したいときは,$x$ に $x-p$,$y$ に $y-q$ を代入する
●頂点を利用した対称移動のポイント
1.頂点を対称移動する
2.$x^2$ の係数($a$ の値)について
$y$ 軸に関する対称移動は符号が変わらない
$x$ 軸,原点に関する対称移動は符号が変わる
●式変形のみで対称移動する方法
$x$ 軸に関して対称移動したいときは $y$ を $-y$ にする
$y$ 軸に関して対称移動したいときは $x$ を $-x$ にする
原点に関して対称移動したいときは $x$ を $-x$,$y$ を $-y$ にする




コメント