10 進法

普段使っている $10$ 進法について,詳しくみてみよう!
$2345$ は千の位を $2$,百の位を $3$,十の位を $4$,一の位を $5$ と考える

$2345=2\cdot10^3+3\cdot10^2+4\cdot10^1+5\cdot10^0$ ($10^0=1$)
- 位の取り方が $10^○$ の位
- 各位の数字が $0,1,2,\cdots,9$ の $10$ 種類
であるような表記方法を $10$ 進法という
$0,1,2,\cdots,9$
$9$ の次は一の位だけで表せないから十の位をつくる
$10,11,12,\cdots,99$
$99$ の次は十の位だけで表せないから百の位をつくる
$100,101,102,\cdots,999$
$999$ の次は百の位だけで表せないから千の位をつくる
以上のように,$10$ 進法では $10^○$ ごとに位が上がる
2 進法

$10$ 進法の $10$ が $2$ になったと考えよう!

$2$ 進法は $0$ と $1$ しか使えないんだね!

$0$ から順番に書いていくとこんな感じ!
| $10$ 進法 | $2$ 進法 |
| $0$ | $0$ |
| $1$ | $1$ |
| $2$ | $10$ |
| $3$ | $11$ |
| $4$ | $100$ |
| $5$ | $101$ |
| $6$ | $110$ |
| $7$ | $111$ |
| $8$ | $1000$ |
| $9$ | $1001$ |
| $10$ | $1010$ |
| $11$ | $1011$ |
| $12$ | $1100$ |
| $13$ | $1101$ |
| $14$ | $1110$ |
| $15$ | $1111$ |
| $16$ | $10000$ |
| $17$ | $10001$ |
| $18$ | $10010$ |
| $19$ | $10011$ |
| $20$ | $10100$ |
| $21$ | $10101$ |
| $22$ | $10110$ |
| $23$ | $10111$ |
| $24$ | $11000$ |
| $25$ | $11001$ |
| $26$ | $11010$ |
| $27$ | $11011$ |
| $28$ | $11100$ |
| $29$ | $11101$ |
| $30$ | $11110$ |
| $31$ | $11111$ |
| $32$ | $100000$ |
$2$ 進法で位が上がるところをみてみると
| $10$ 進法 | $2$ 進法 |
| $2$ | $10$ |
| $4$ | $100$ |
| $8$ | $1000$ |
| $16$ | $10000$ |
| $32$ | $100000$ |
$2=2^1$,$4=2^2$,$8=2^3$,$16=2^4$,$32=2^5$
$2^○$ ごとに位が上がるので,位の取り方が $2^○$ の位
$2$ 進法で表記していることを表すために,
$2$ 進法で $10110$ を $10110_{(2)}$ と表す
2 進法を 10 進法にする
$10$ 進法の $2345$ は位取りが $10^○$ なので
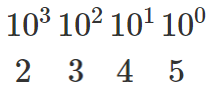
$2345=2\cdot10^3+3\cdot10^2+4\cdot10^1+5\cdot10^0$ ($10^0=1$)
と表せる
これを $2$ 進法で用いれば,$2$ 進法を $10$ 進法で表すことができる

$2$ 進法は位取りが $2^○$ であることを使おう!
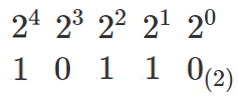
$10110_{(2)}=1\cdot2^4+0\cdot2^3+1\cdot2^2+1\cdot2^1+0\cdot2^0$ ($2^0=1$)
$=16+0+4+2+0$
$=22$

位取りができれば,$10$ 進法で表せるね!
3 進法

$3$ 進法は $0,1,2$ しか使えないんだね!

$0$ から順番に書いていくとこんな感じ!
| $10$ 進法 | $3$ 進法 |
| $0$ | $0$ |
| $1$ | $1$ |
| $2$ | $2$ |
| $3$ | $10$ |
| $4$ | $11$ |
| $5$ | $12$ |
| $6$ | $20$ |
| $7$ | $21$ |
| $8$ | $22$ |
| $9$ | $100$ |
| $10$ | $101$ |
| $11$ | $102$ |
| $12$ | $110$ |
| $13$ | $111$ |
| $14$ | $112$ |
| $15$ | $120$ |
| $16$ | $121$ |
| $17$ | $122$ |
| $18$ | $200$ |
| $19$ | $201$ |
| $20$ | $202$ |
| $21$ | $210$ |
| $22$ | $211$ |
| $23$ | $212$ |
| $24$ | $220$ |
| $25$ | $221$ |
| $26$ | $222$ |
| $27$ | $1000$ |
$3$ 進法で位が上がるところをみてみると
| $10$ 進法 | $3$ 進法 |
| $3$ | $10$ |
| $9$ | $100$ |
| $27$ | $1000$ |
$3=3^1$,$9=3^2$,$27=3^3$
$3^○$ ごとに位が上がるので,位の取り方が $3^○$ の位
$3$ 進法で表記していることを表すために,
$3$ 進法で $212$ を $212_{(3)}$ と表す
3 進法を 10 進法にする

$3$ 進法は位取りが $3^○$ であることを使おう!
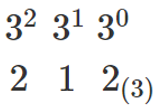
$212_{(3)}=2\cdot3^2+1\cdot3^1+2\cdot3^0$ ($3^0=1$)
$=18+3+2$
$=23$

$3$ 進法は位取りが $3^○$!
n 進法
$2$ 進法や $3$ 進法と同様すれば,
$4$ 進法,$5$ 進法,$\cdots$ も $10$ 進法で表すことができる
まとめ
● $10$ 進法
- 位の取り方が $10^○$ の位
- 各位の数字が $0,1,2,\cdots,9$ の $10$ 種類
● $2$ 進法
- 位の取り方が $2^○$ の位
- 各位の数字が $0,1$ の $2$ 種類
● $3$ 進法
- 位の取り方が $3^○$ の位
- 各位の数字が $0,1,2$ の $3$ 種類
● $n$ 進法
- 位の取り方が $n^○$ の位
- 各位の数字が $0,1,2,\cdots,n-1$ の $n$ 種類
問題
(1) $101101_{(2)}$
(2) $12102_{(3)}$
(3) $241_{(5)}$
(1) $101101_{(2)}$
$101101_{(2)}=1\cdot2^5+0\cdot2^4+1\cdot2^3+1\cdot2^2+0\cdot2^1+1\cdot2^0$
$=32+0+8+4+0+1$
$=45$
(2) $12102_{(3)}$
$12102_{(3)}=1\cdot3^4+2\cdot3^3+1\cdot3^2+0\cdot3^1+2\cdot3^0$
$=81+54+9+0+2$
$=146$
(3) $241_{(5)}$
$241_{(5)}=2\cdot5^2+4\cdot5^1+1\cdot5^0$
$=50+20+1$
$=71$

これで $n$ 進法を $10$ 進法で表す問題は完璧!




コメント