データの代表値

データ全体の特徴を1つの数値で表したものを代表値というよ!
代表値として,「平均値」「最頻値」「中央値」を学ぼう!
平均値

平均値はよく使うからわかるよ!
データを全部足して,データの大きさ(個数)で割ったら求まる!
$n$ 個の変量 $x$ のデータ $x_1$,$x_2$,$x_3$,$……$,$x_n$ の平均値 $\bar{x}$ は
$\displaystyle\bar{x}=\frac{1}{n}(x_1+x_2+x_3+……+x_n)$

平均値は $\bar{ }$ が使われることは覚えておこう!
最頻値
$5$ 個のデータ $3,4,4,5,6$ の最頻値は $4$ である
中央値

中央値は文字通り中央の値だね!

その通りだけど,データの個数が偶数個のときは注意が必要!
大きさの順に並べたとき,中央に位置する値
偶数個のときは中央にくる2つの値の平均をとって中央値とする
● 奇数個のとき … 中央が1つ

$5$ 個のデータ $3,4,6,8,9$ の中央値は $6$ である
● 偶数個のとき…中央が2つ

$6$ 個のデータ $3,4,6,7,8,9$ の中央値は
$6$ と $7$ の平均をとって $6.5$ である

中央値は四分位数でも使うので,きちんと理解しておこう!
四分位数

四分位数はデータを4等分する位置にくる値のこと!
四分位数には3つの値があるよ!
四分位数は,小さい方から順に
第1四分位数,第2四分位数(中央値),第3四分位数 という
順に $Q_1$,$Q_2$,$Q_3$ で表す
$Q_2$ は中央にくるので中央値と等しい
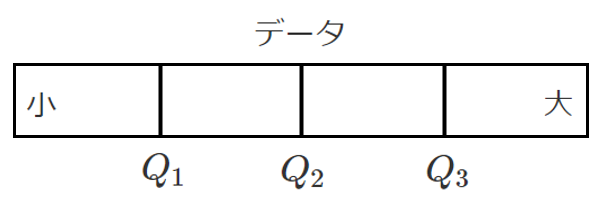
四分位数の求め方
● 奇数個のとき
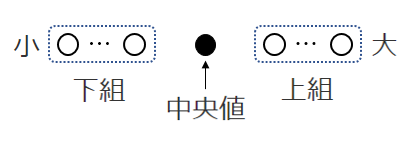
- 小さい順に並べて中央値 $Q_2$ を求める
- 中央値を除いて下組と上組に分ける
- 下組の中央値が $Q_1$,上組の中央値が $Q_3$
● 偶数個のとき
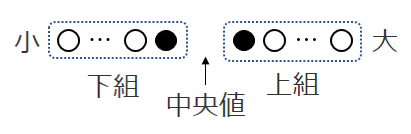
- 小さい順に並べて中央にくる2つの値の平均をとって中央値 $Q_2$ を求める
- 下組と上組に分ける
- 下組の中央値が $Q_1$,上組の中央値が $Q_3$
問題
次のデータの四分位数を求めよ。
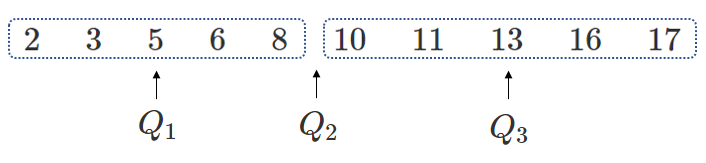
(1) $2 3 5 6 8 10 11$
(2) $2 3 5 6 8 10 11 13$
(3) $2 3 5 6 8 10 11 13 16$
(4) $2 3 5 6 8 10 11 13 16 17$
(1) $Q_1=3$,$Q_2=6$,$Q_3=10$
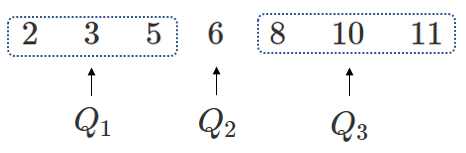
(2) $Q_1=4$,$Q_2=7$,$Q_3=10.5$
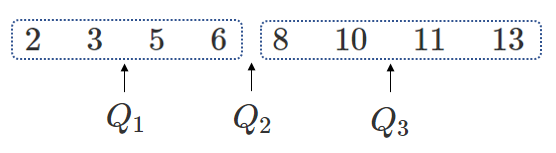
(3) $Q_1=4$,$Q_2=8$,$Q_3=12$
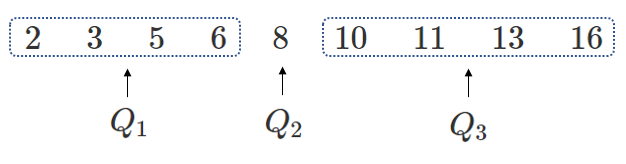
(4) $Q_1=5$,$Q_2=9$,$Q_3=13$

求め方が分かれば簡単だね!
中央値をきちんと理解することが大切!
四分位範囲と四分位偏差
四分位範囲 $Q_3-Q_1$
四分位偏差 $\displaystyle\frac{Q_3-Q_1}{2}$$\left(\displaystyle\frac{四分位範囲}{2}\right)$

どっちがどっちか分からなくなるので注意!
四分位範囲が 「$Q_3-Q_1$」
四分位偏差が 「四分位範囲÷2」と覚えておこう!
問題
次のデータの四分位範囲と四分位偏差を求めよ。
$2 3 5 6 8 10 11$
$Q_1=3$,$Q_2=6$,$Q_3=10$

四分位範囲は $Q_3-Q_1=10-3=7$
四分位偏差は $\displaystyle\frac{7}{2}=3.5$
まとめ
● 平均値
$\displaystyle(平均値)=\frac{(データの総和)}{(データの大きさ)}$
● 最頻値
データにおいて,最も個数が多い値
● 中央値
大きさの順に並べたとき,中央に位置する値
偶数個のときは中央にくる2つの値の平均をとって中央値とする
● 四分位数
小さい方から順に第1四分位数,第2四分位数(中央値),第3四分位数 という
順に $Q_1$,$Q_2$,$Q_3$ で表し,$Q_2$ は中央にくるので中央値と等しい
● 奇数個のときの四分位数の求め方

- 小さい順に並べて中央値 $Q_2$ を求める
- 中央値を除いて下組と上組に分ける
- 下組の中央値が $Q_1$,上組の中央値が $Q_3$
● 偶数個のときの四分位数の求め方

- 小さい順に並べて中央にくる2つの値の平均をとって中央値 $Q_2$ を求める
- 下組と上組に分ける
- 下組の中央値が $Q_1$,上組の中央値が $Q_3$
● 四分位範囲と四分位偏差
四分位範囲 $Q_3-Q_1$
四分位偏差 $\displaystyle\frac{Q_3-Q_1}{2}$$\left(\displaystyle\frac{四分位範囲}{2}\right)$

四分位数の求め方はきちんとおさえておかないとね!




コメント