
ユークリッドの互除法は「最大公約数」を求めるための方法!
互除法以外に最大公約数を求める方法はこれ↓


互除法で最大公約数を求める場面

最大公約数を求める方法は分かっているのに,互除法をわざわざ使う必要あるの?

次の問題を考えてみよう!

素因数分解が簡単にできない…

そうだね!
ちなみに素因数分解をすると,
$493=17\cdot29$
$391=17\cdot23$
になるから最大公約数は $17$ だよ!
素因数分解が簡単にできないときが互除法を使う場面だと考えよう!
互除法の考え方の基になる定理
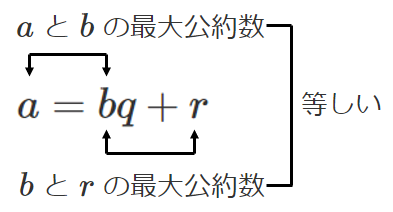
$a$ と $b$ の最大公約数は,$b$ と $r$ の最大公約数に等しい
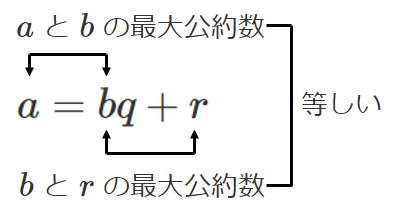
$48$ と $36$ について
$48=36\cdot1+12$
$(48 と 36 の最大公約数)=(36 と 12 の最大公約数)$
どちらも最大公約数は $12$
$184$ と $69$ について
$184=69\cdot2+46$
$(184 と 69 の最大公約数)=(69 と 46 の最大公約数)$
$184=23\cdot8$
$69=23\cdot3$
$46=23\cdot2$ より
どちらも最大公約数は $23$

具体例をみると,たしかにこの定理は成り立ちそうだね!
互除法を使って最大公約数を求める

上の定理を繰り返し用いて最大公約数を求めてみよう!
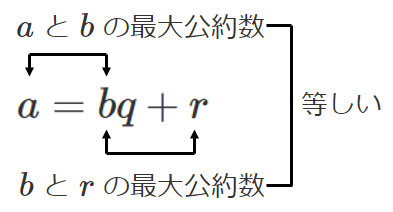
① $184$ を $69$ で割る
$184=69\cdot2+46$
$(184 と 69 の最大公約数)=(69 と 46 の最大公約数)$
② $69$ を $46$ で割る
$69=46\cdot1+23$
$(69 と 46 の最大公約数)=(46 と 23 の最大公約数)$
③ $46$ を $23$ で割る
$46=23\cdot2$
$(46 と 23 の最大公約数)=23$
①,②,③ をつなげると
$(184 と 69 の最大公約数)$
$=(69 と 46 の最大公約数)$
$=(46 と 23 の最大公約数)$
$=23$
つまり,$184$ と $69$ の最大公約数は $23$
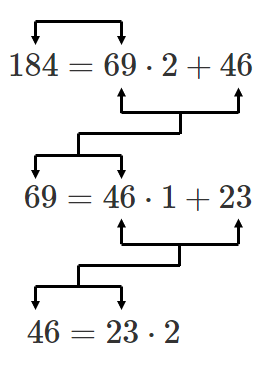

順番に割り算していくと,最後に最大公約数が求まるんだね!
互除法を図形で考える
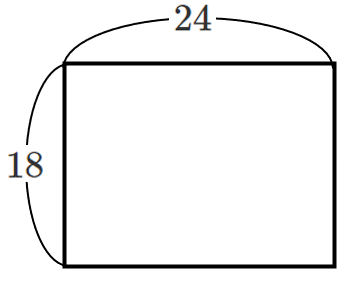

敷き詰めることができる正方形の1辺の長さは,
$1$,$2$,$3$,$6$ だから,
最も大きい正方形の1辺の長さは $6$ になる!
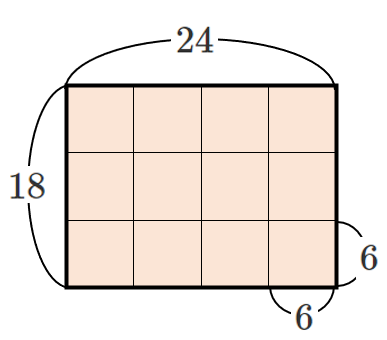

その通り!
この問題の答えは,縦の長さ $18$ と横の長さ $24$ の最大公約数の $6$ が答えになるね!
横の長さが $184$,縦の長さが $69$ の長方形を考える
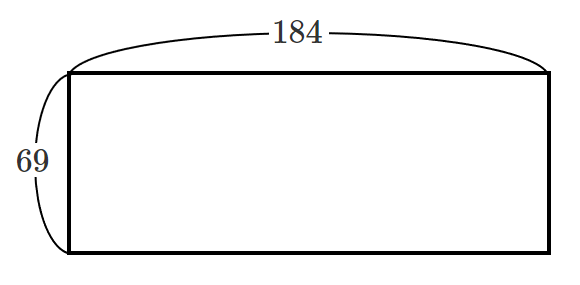
$184$ と $69$ の最大公約数 $g$ とすると
1辺の長さ $g$ の正方形が長方形を敷き詰めることができる最も大きい正方形である
以下で互除法の式を図でみていく
① $184=69\cdot2+46$
1辺の長さが $69$ の正方形を敷き詰めると
縦の長さ $69$,横の長さ $46$ の長方形が残る
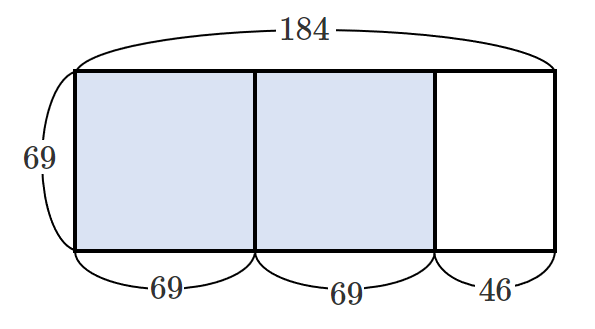
② $69=46\cdot1+23$
①で残った縦の長さ $69$,横の長さ $46$ の長方形を
1辺の長さが $46$ の正方形を敷き詰めると
縦の長さ $23$,横の長さ $46$ の長方形が残る
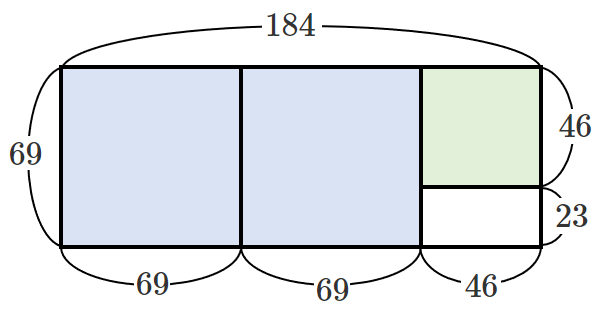
③ $46=23\cdot2$
②で残った縦の長さ $23$,横の長さ $46$ の長方形を
1辺の長さが $23$ の正方形で敷き詰めると
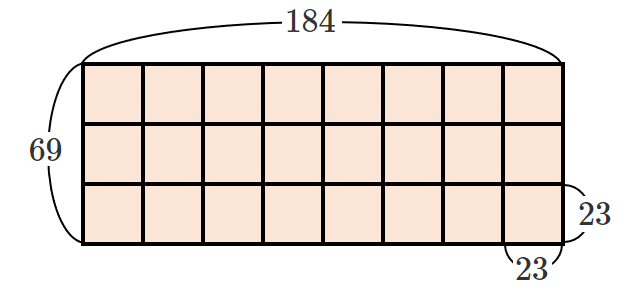
横の長さが $184$,縦の長さが $69$ の長方形が埋まる
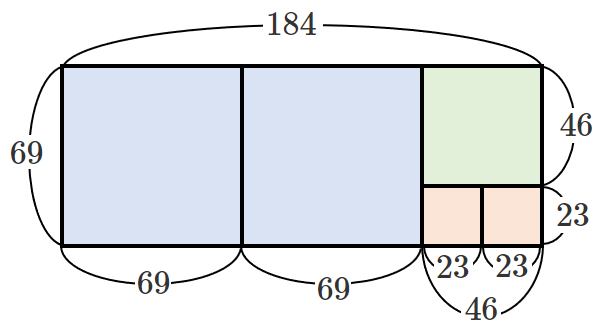
最後に敷き詰めた1辺の長さ $23$ の正方形が
横の長さ $184$,縦の長さ $69$ の長方形を敷き詰めることができる最大の正方形である
まとめ
● 互除法の考えの基になる定理
● 互除法
上の定理を繰り返して最大公約数を求める方法を互除法という
問題
(1) $391$ と $161$
(2) $493$ と $391$
(1)
$391=161\cdot2+69$
$161=69\cdot2+23$
$69=23\cdot3$
$391$ と $161$の最大公約数は $23$
(2)
$493=391\cdot1+102$
$391=102\cdot3+85$
$102=85\cdot1+17$
$85=17\cdot5$
$493$ と $391$の最大公約数は $17$

ややこしそうに見えるけど,割り算を繰り返しているだけ!
しっかり練習しよう!




コメント