
三角形の外心・内心・重心を整理しよう!
三角形の外心
三角形の各辺について,辺の垂直二等分線を引くと
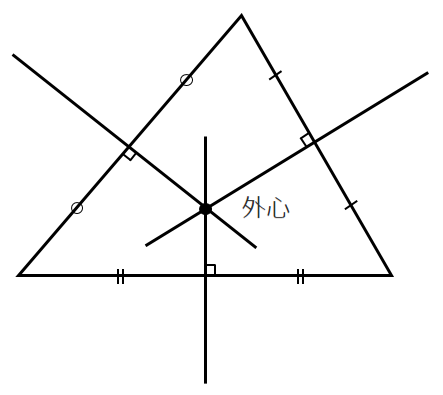
辺の垂直二等分線は1点で交わる
その交点を「外心」とする
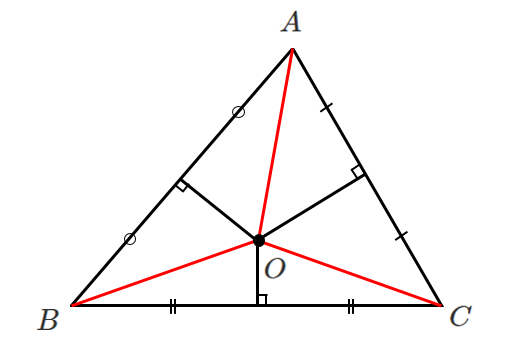
外心を点 $O$ とすると
$\triangle OAB$ と $\triangle OBC$ と$\triangle OCA$ は二等辺三角形となり
$OA=OB=OC$ が成り立つ
点 $O$ にコンパスの針を当てて
$OA$ を半径にして円を描くと
$\triangle ABC$ の外接円になる
点 $O$ (外心) は $\triangle ABC$ の外接円の中心である
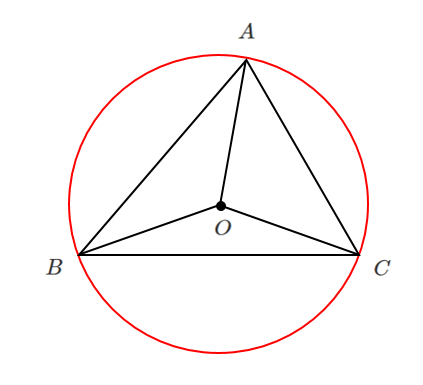

三角形の外接円の中心だから「外心」!
辺の垂直二等分線の交点!
三角形の内心
三角形について,角の二等分線を引くと
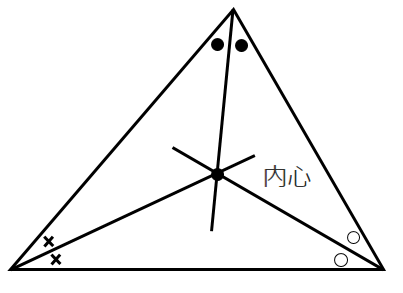
角の二等分線は1点で交わる
その交点を「内心」とする
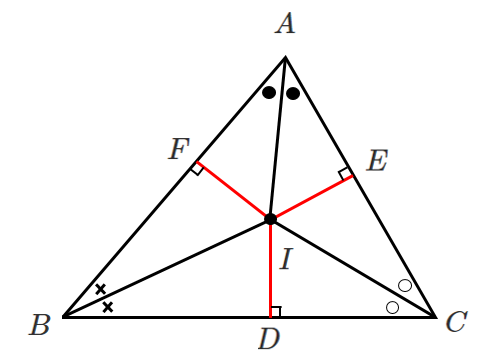
内心を点 $I$ とすると
$\triangle BFI \equiv \triangle BDI$ より $IF=ID$
$\triangle CDI \equiv \triangle CEI$ より $ID=IE$
$\triangle AEI \equiv \triangle AFI$ より $IE=IF$
よって $ID=IE=IF$ が成り立つ
点 $I$ にコンパスの針を当てて
$OD$ を半径にして円を描くと
$\triangle ABC$ の内接円になる
点 $I$ (内心) は $\triangle ABC$ の内接円の中心である
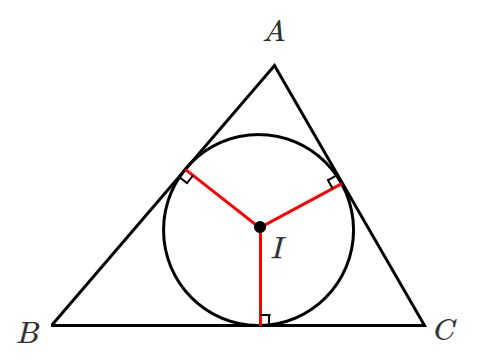

三角形の内接円の中心だから「内心」!
角の二等分線の交点!
三角形の重心
中線 … 三角形の頂点とそれに向かい合う辺の中点を結ぶ線分
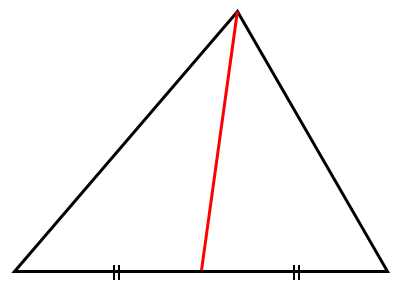
三角形について,中線を引くと
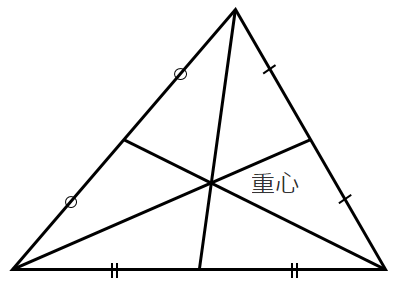
中線は1点で交わる
この交点を「重心」という
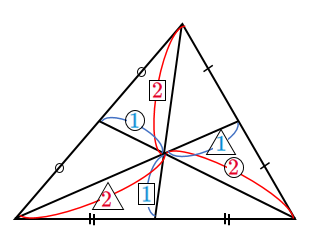
重心は各中線を $2:1$ に内分する
まとめ
● 三角形の外心
- 辺の垂直二等分線の交点
- 三角形の外接円の中心
● 三角形の内心
- 角の二等分線の交点
- 三角形の内接円の中心
● 三角形の重心
- 中線の交点
- 各中線を $2:1$ に内分する

三角形の外心・内心・重心がそれぞれどういう点かをきちんと覚えておこう!
外心と内心がごちゃごちゃにならないように注意しよう!




コメント