三角形の外角の二等分線と比

「三角形の内角の二等分線と比」と似ているよ！

「三角形の内角の二等分線と比」の定理はこれ↓

リンク

三角形の外角の二等分線と比の定理

$AB\neq AC$ である $\triangle ABC$ の $\angle A$ の外角の二等分線と辺 $BC$ の延長と交点を $D$ とすると
　$AB:AC=BD:DC$　が成り立つ

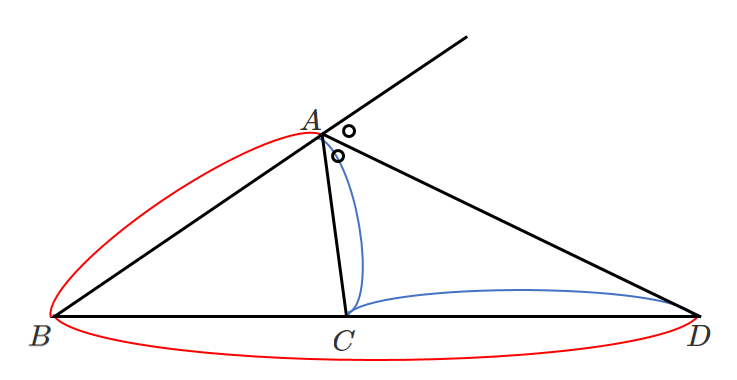
$AB$$:$$AC$$=$$BD$$:$$DC$

点 $D$ は辺 $BC$ を $AB:AC$ に外分する点になるよ！

$\angle A$ の外角の二等分線と辺 $BC$ の延長との交点を $D$ とし，

頂点 $C$ を通り，直線 $AD$ に平行な直線を引き，辺 $AB$ との交点を $E$ とする

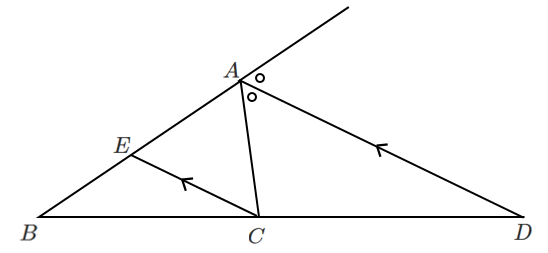
辺 $AB$ の $A$ を越える延長上に $F$ をとると

$\angle CAD=\angle FAD$　$\cdots$　①

$AD/\!/EC$ より

$\angle CAD=\angle ACE$　(錯覚)　$\cdots$　②

$\angle AEC=\angle FAD$　(同位角)　$\cdots$　③

①，②，③より，$\triangle ACE$ において

$\angle ACE=\angle AEC$　が成り立つので　$AC=AE$

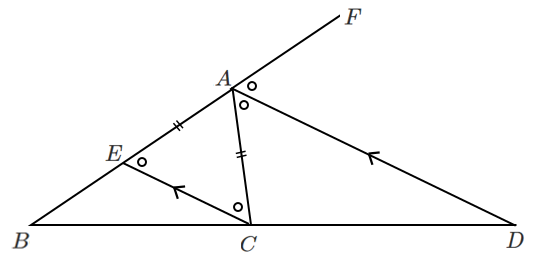
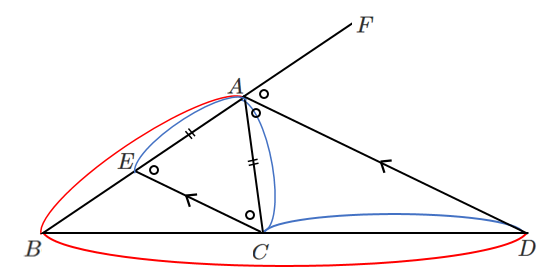
$AD/\!/EC$ より

$AB$$:$$AE$$=$$BD$$:$$DC$

$AC=AE$ より　$AB$$:$$AC$$=$$BD$$:$$DC$

$AB=8$，$AC=6$，$BC=4$ である $\triangle ABC$ において，$\angle A$ の外角の二等分線と辺 $BC$ の延長との交点を $D$ とするとき，$BD$ の長さを求めよ。

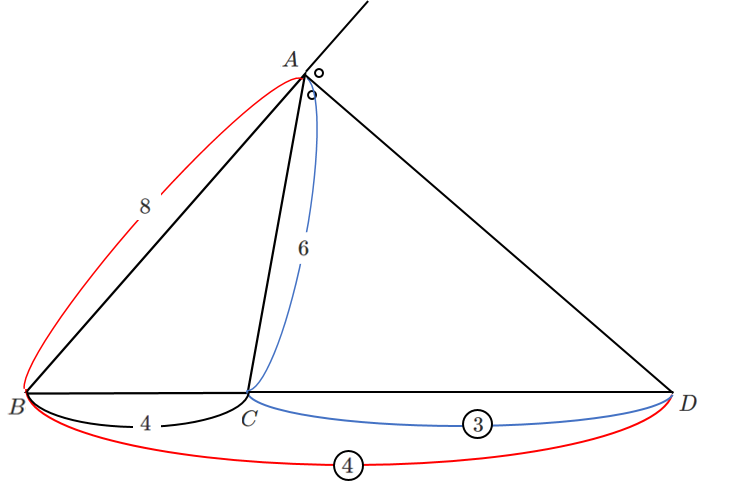
$AD$ は $\angle A$ の外角の二等分線だから

$BD:DC=AB:AC=8:6=4:3$

$BD$ の長さは　$\displaystyle{BD=4\times BC=16}$

内角の二等分線は内分点！

外角の二等分線は外分点！