三角形の面積の公式といえば,「底辺×高さ÷2」
しかし,三角形の面積を計算する問題で,底辺と高さがわかっているケースは少ないです!
高校数学において,三角形の面積を求める際には,sinを用いた公式をよく使います!
sinを用いた公式を使えば,2辺とその間の角のsinで三角形の面積を求めることができます!
この投稿では,sinを用いた三角形の面積の公式の使い方と証明をわかりやすく解説します!

三角形の面積といえば,
「底辺×高さ÷2」だったよね!
三角比を用いた三角形の面積の求め方を学ぼう!
三角形の面積
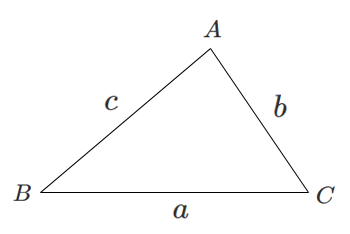
$\triangle ABC$ の面積 $S$
$$\displaystyle S=\frac{1}{2}bc\sin A$$
$$\displaystyle S=\frac{1}{2}ca\sin B$$
$$\displaystyle S=\frac{1}{2}ab\sin C$$

シンプルにすると以下のようになるよ!
$\displaystyle S=\frac{1}{2}〇□\sin\theta$
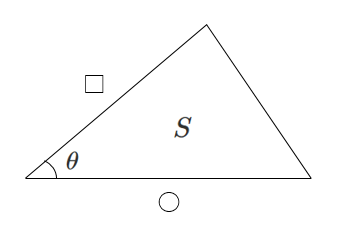
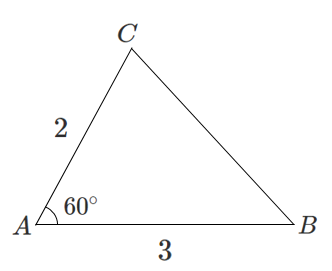
問題
三角形の面積の公式の証明

$\displaystyle S=\frac{1}{2}bc\sin A$ はどうやったら導くことができるのかな?
$\triangle ABC$ において,辺 $AB$ を底辺とするときの高さを $h$ とすると
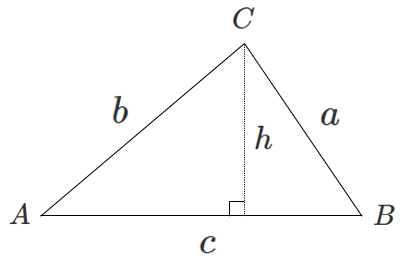
$\displaystyle\sin A=\frac{h}{b}$ より $h=b\sin A$
この式が分からない人はこれ↓

$\displaystyle S=\frac{1}{2}ch$ より $\displaystyle S=\frac{1}{2}bc\sin A$
三角形の3辺の長さと面積

三角形の3辺の長さがわかっていれば,
三角形の面積が求まるよ!
- 余弦定理で $\cos$ の値を求める
- $\sin^2\theta+\cos^2\theta=1$ で,1で求めた $\cos$ の値から $\sin$ の値を求める
- $\displaystyle S=\frac{1}{2}○□\sin\theta$ を用いて面積を求める
余弦定理の復習はこれ↓
$\sin^2\theta+\cos^2\theta=1$ の復習はこれ↓

問題
$\sin^2 A+\cos^2 A=1$ より
\begin{eqnarray} \sin^2 A &=& 1-\cos^2 A \\\\ &=& 1-\left(\frac{3}{4}\right)^2 \\\\ &=& \frac{7}{16} \end{eqnarray}$0^\circ<A<180^\circ$ より $\sin A>0$
よって $\displaystyle\sin A=\frac{\sqrt{7}}{4}$
\begin{eqnarray} S &=& \frac{1}{2}・4・3・\sin A \\\\ &=& \frac{1}{2}・4・3・\frac{\sqrt{7}}{4} \\\\ &=& \frac{3\sqrt{7}}{2} \end{eqnarray}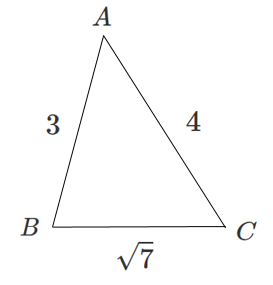
まとめ
● 三角形の面積
$$\displaystyle S=\frac{1}{2}〇□\sin\theta$$

● 三角形の3辺の長さから面積を求める手順
- 余弦定理で $\cos$ の値を求める
- $\sin^2\theta+\cos^2\theta=1$ で,1で求めた $\cos$ の値から $\sin$ の値を求める
- $\displaystyle S=\frac{1}{2}○□\sin\theta$ を用いて面積を求める

三角形の3辺から面積を求める手順の中には,
三角比の重要事項がたくさん含まれているね!
しっかり練習しよう!




コメント