鈍角の三角比の考え方きちんと理解していますか?
鋭角の三角比は直角三角形で考えていましたが,鈍角の三角比は座標で考えるので少し難しく感じます!
ですが,基本をきちんとおさえることで必ず理解できます!
単位円を使った鈍角の三角比の考え方をわかりやすく解説します!

$ 0^\circ≦\theta≦180^\circ$ の三角比を考えてみよう!
鋭角の三角比の定義

鋭角($ 0^\circ<\theta<90^\circ$) の三角比は直角三角形で定義されていたね!
直角三角形の鋭角($90^\circ$ 未満の角)の1つを $\theta$ とし,斜辺の長さを $r$ ,その他の辺の長さを下図のように $x$,$y$ とするとき,三角比の定義は以下のようになる。
※ $x$ のことを $\theta$ の隣の辺なので「隣辺」,$y$ のことを $\theta$ の向かいの辺なので「対辺」とよぶこともある。
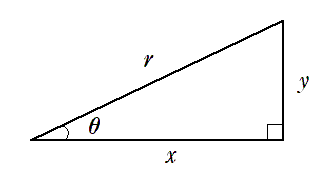
$\displaystyle{\sin\theta=\frac{y}{r}}$, $\displaystyle{\cos\theta=\frac{x}{r}}$, $\displaystyle{\tan\theta=\frac{y}{x}}$
● $\sin\theta$ の覚え方
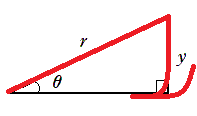
$s$ の筆記体で $\displaystyle{\sin\theta=\frac{y}{r}}$
● $\cos\theta$ の覚え方
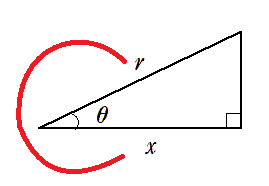
$c$ と書いて $\displaystyle{\cos\theta=\frac{x}{r}}$
● $\tan\theta$ の覚え方
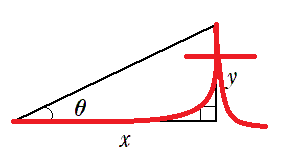
$t$ の筆記体で $\displaystyle{\tan\theta=\frac{y}{x}}$
詳しく復習したい人はこれ↓

座標を用いた三角比の定義

直角三角形だと 90° までしか三角比が定義できないね!
90° より大きい角の三角比はどうやって定義するのかな?

90° より大きい角の三角比は,座標を用いて定義するよ!
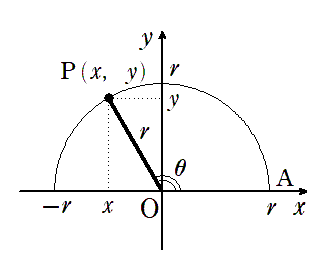
座標平面上において原点を中心とする半径 $r$ の半円をかき,この半円と $x$ 軸の正の部分との交点を $A$ とする。
$∠AOP=\theta$ となる点 $P$ をこの半円上にとり,点 $P$ の座標を $(x,y)$ としたとき,
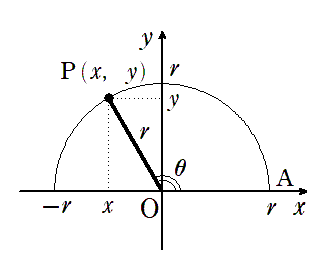

結局,鋭角($ 0^\circ<\theta<90^\circ$) の三角比と定義の式は同じだね!

大まかにみると同じだけど,
$x$ と $y$ が長さではなく座標になったことは注意しよう!
単位円による三角比の定義

$r=1$ の円(単位円)を考えると,$\sin\theta$ と $\cos\theta$ の定義がシンプルになるよ!
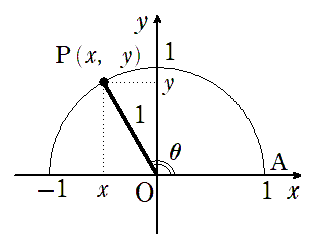
$$\sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r}$$
$$ \Downarrow r=1とする$$
$$\sin\theta=y,\cos\theta=x$$
$\sin\theta$ は単位円上の点の $y$ 座標,$\cos\theta$ は単位円上の点の $x$ 座標
用いる直角三角形
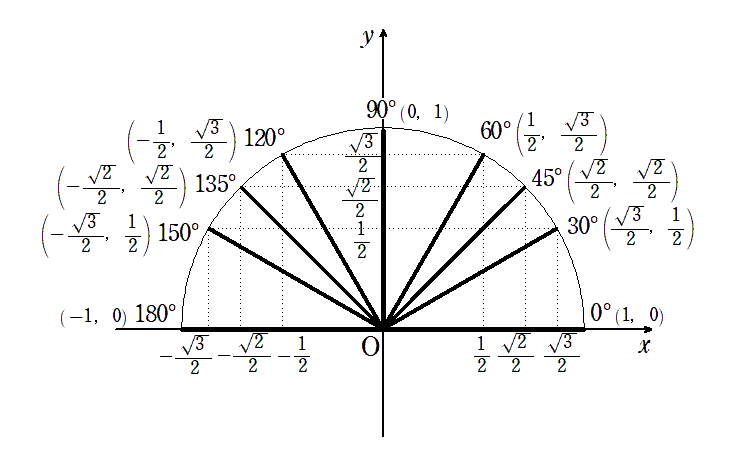
30$^\circ$,45$^\circ$,60$^\circ$ の直角三角形の斜辺の長さを $1$ にすると
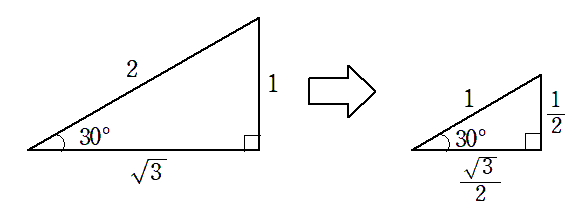
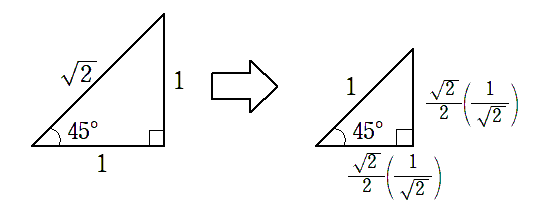
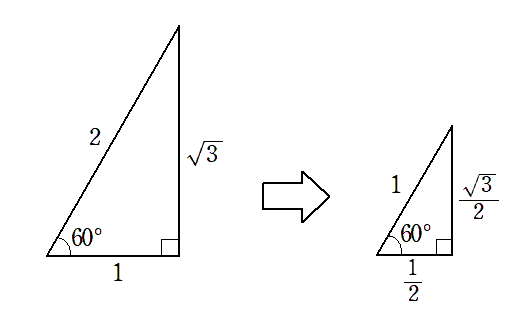
$\sin\theta$,$\cos\theta$ の値
$\sin\theta$ は $y$ 座標
$\cos\theta$ は $x$ 座標
● $\sin0^\circ=0$,$\cos0^\circ=1$
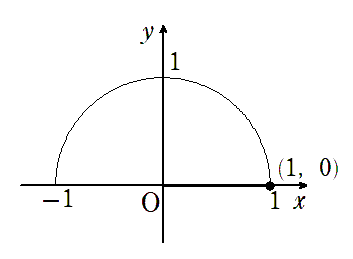
● $\displaystyle{\sin30^\circ=\frac{1}{2}}$,$ \displaystyle{ \cos30^\circ=\frac{\sqrt{3}}{2}}$
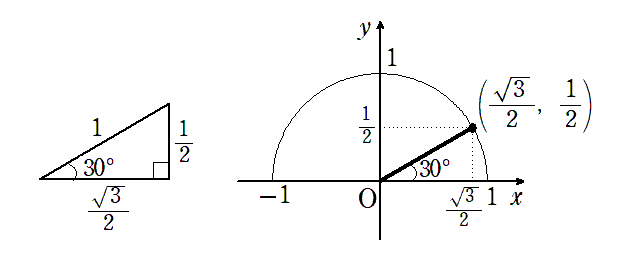
● $ \displaystyle{ \sin45^\circ=\frac{\sqrt{2}}{2}}$,$ \displaystyle{ \cos45^\circ=\frac{\sqrt{2}}{2}}$
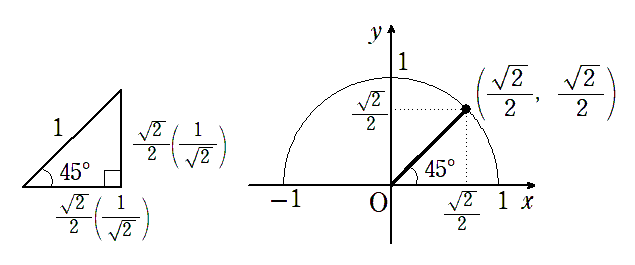
実際,$ \displaystyle{ \frac{1}{\sqrt{2}}}$ と書くことが多いですが,
大小関係を分かりやすくするために $ \displaystyle{ \frac{\sqrt{2}}{2}}$ と書いています
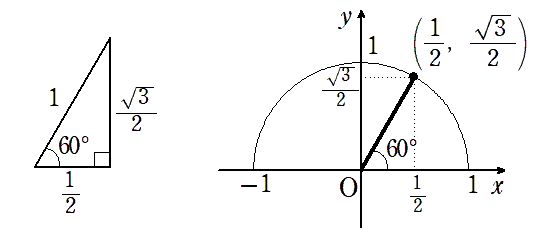
● $ \displaystyle{ \sin60^\circ=\frac{\sqrt{3}}{2}}$,$ \displaystyle{ \cos60^\circ=\frac{1}{2}}$
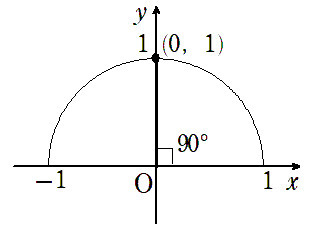
● $\sin90^\circ=1$,$\cos90^\circ=0$
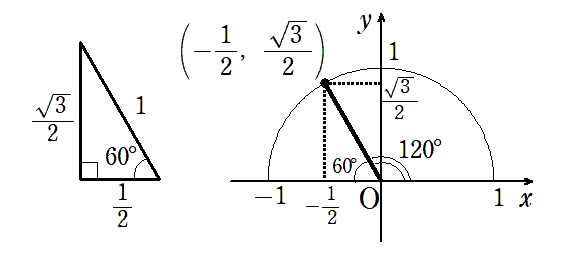
● $ \displaystyle{ \sin120^\circ=\frac{\sqrt{3}}{2}}$,$ \displaystyle{ \cos120^\circ=-\frac{1}{2}}$
● $ \displaystyle{ \sin135^\circ=\frac{\sqrt{2}}{2}}$,$ \displaystyle{ \cos135^\circ=-\frac{\sqrt{2}}{2}}$
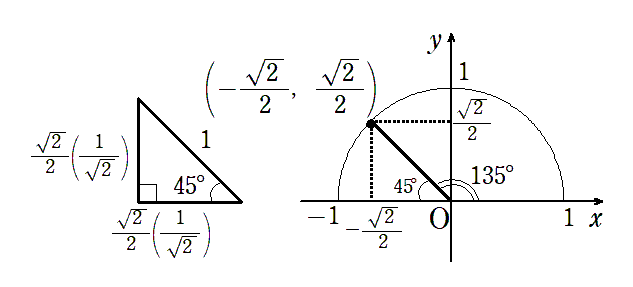
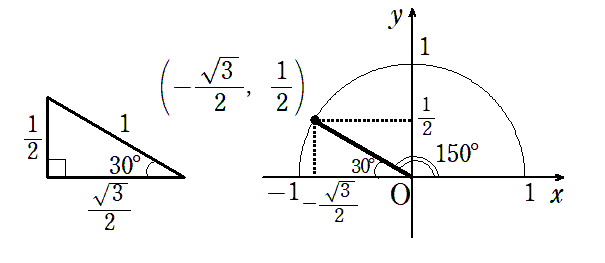
● $ \displaystyle{ \sin150^\circ=\frac{1}{2}}$,$ \displaystyle{ \cos150^\circ=-\frac{\sqrt{3}}{2}}$
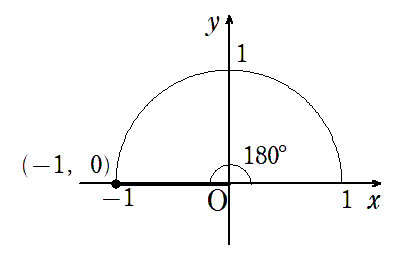
● $\sin180^\circ=0$,$\cos180^\circ=-1$
| $\theta$ | $ 0^\circ$ | $ 30^\circ$ | $ 45^\circ$ | $ 60^\circ$ | $ 90^\circ$ | $ 120^\circ$ | $ 135^\circ$ | $ 150^\circ$ | $ 180^\circ$ |
| $\sin\theta$ | $0$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ |
| $\cos\theta$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ | $-\frac{1}{2}$ | $-\frac{\sqrt{2}}{2}$ | $-\frac{\sqrt{3}}{2}$ | $-1$ |
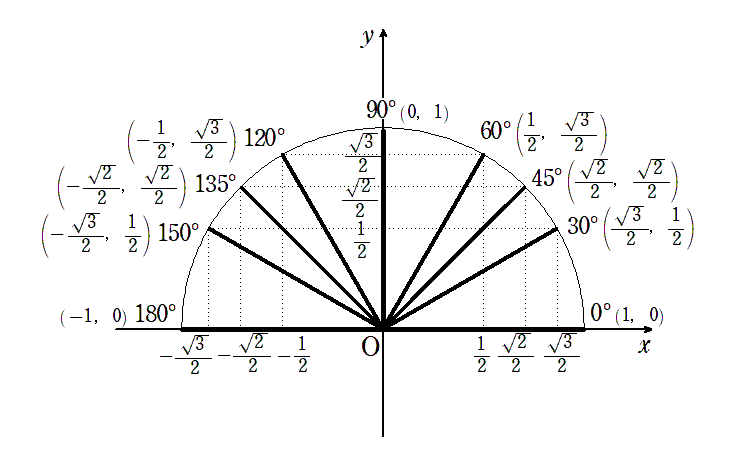
$\sin\theta$ は $y$ 座標なので,$\theta$ が大きくなるにつれて,
$ 90^\circ$ までは大きくなり,$ 90^\circ$ 以降は小さくなる
$\cos\theta$ は $x$ 座標なので,$\theta$ が大きくなるにつれて,小さくなる
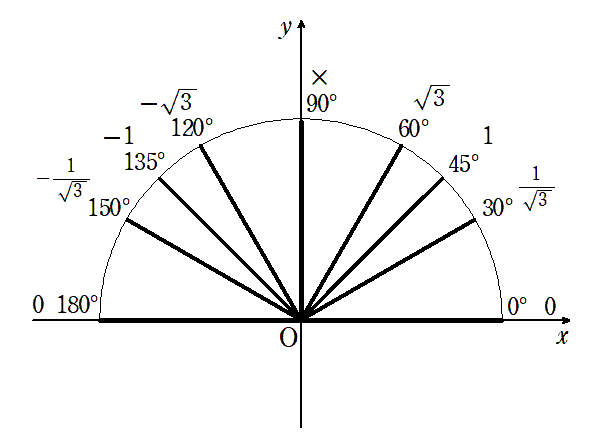
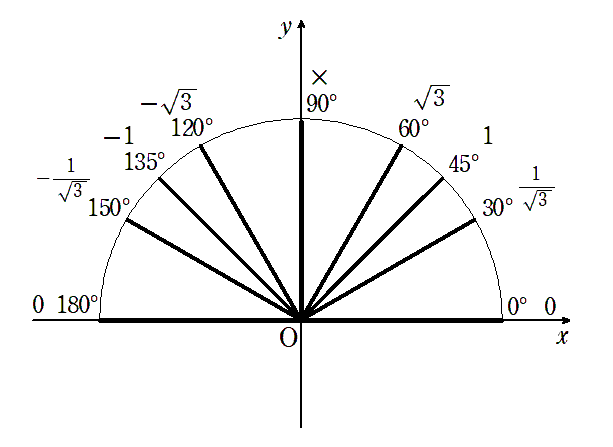
$\tan\theta$ の値
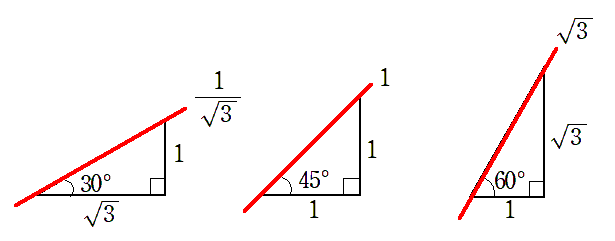
$\tan\theta$ は $ \displaystyle{ \frac{y}{x}}$ なので,$\tan\theta$ は直角三角形の斜辺の傾きを表している
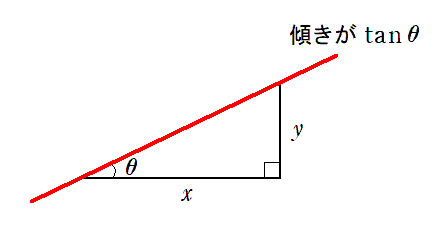
$\tan\theta$ は傾き
● $ \displaystyle{ \tan30^\circ=\frac{1}{\sqrt{3}}}$,$\tan45^\circ=1$,$ \tan60^\circ=\sqrt{3}$
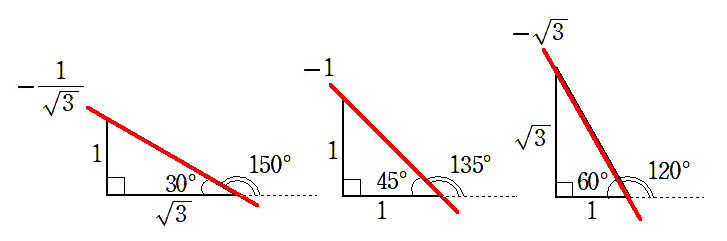
● $\tan120^\circ=-\sqrt{3}$,$\tan135^\circ=-1$,$ \displaystyle{ \tan150^\circ=-\frac{1}{\sqrt{3}}}$
● $\tan0^\circ=0$,$\tan180^\circ=0$
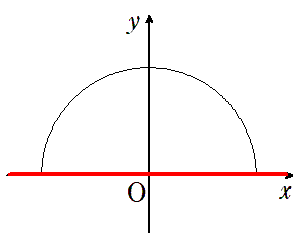
$ 0^\circ$,$ 180^\circ$ のときの傾きは $0$
(全く傾いていない)
● $\tan90^\circ$ はなし
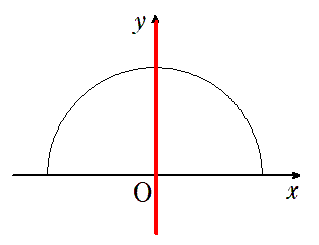
$ 90^\circ$ のときの傾きは「定義できない」
(傾きすぎ)
| $\theta$ | $ 0^\circ$ | $ 30^\circ$ | $ 45^\circ$ | $ 60^\circ$ | $ 90^\circ$ | $ 120^\circ$ | $135^\circ$ | $ 150^\circ$ | $ 180^\circ$ |
| $\tan\theta$ | $0$ | $\frac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ | × | $-\sqrt{3}$ | $-1$ | $-\frac{1}{\sqrt{3}}$ | $0$ |
三角比の符号

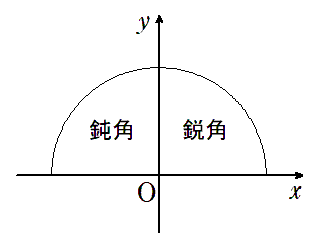
鋭角と鈍角における三角比の符号をきちんとおさえておこう!
| $\theta$ | 鋭角 | 鈍角 |
| $\sin\theta$ | $+$ | $+$ |
| $\cos\theta$ | $+$ | $-$ |
| $\tan\theta$ | $+$ | $-$ |
鋭角は $ 0^\circ<\theta<90^\circ$,鈍角は $ 90^\circ<\theta<180^\circ$

鈍角における $\cos\theta$ と $\tan\theta$ が負になることがポイント!
まとめ
● 三角比の定義
$ \displaystyle{ \sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r},\tan\theta=\frac{y}{x}}$
● $\sin\theta$ は $y$ 座標,$\cos\theta$ は $x$ 座標
($r=1$ とすると)
● $\tan\theta$ は傾き
● 三角比の値
| $\theta$ | $ 0^\circ$ | $ 30^\circ$ | $ 45^\circ$ | $ 60^\circ$ | $ 90^\circ$ | $ 120^\circ$ | $ 135^\circ$ | $ 150^\circ$ | $ 180^\circ$ |
| $\sin\theta$ | $0$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ |
| $\cos\theta$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ | $-\frac{1}{2}$ | $-\frac{\sqrt{2}}{2}$ | $-\frac{\sqrt{3}}{2}$ | $-1$ |
| $\tan\theta$ | $0$ | $\frac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ | × | $-\sqrt{3}$ | $-1$ | $-\frac{1}{\sqrt{3}}$ | $0$ |
● 三角比の符号
| $\theta$ | 鋭角 | 鈍角 |
| $\sin\theta$ | $+$ | $+$ |
| $\cos\theta$ | $+$ | $-$ |
| $\tan\theta$ | $+$ | $-$ |
鈍角における $\cos\theta$ と $\tan\theta$ が負になる

きちんと理解しておけば,数Ⅱの三角関数にも使えるよ!




コメント