三角比の相互関係3つ答えられますか?
その3つはそれぞれどういう場面で使えるか理解していますか?
三角比の相互関係が使いこなせれば,
sin・cos・tanの内の1つから,他の値を求めることができます!
鋭角か鈍角かに注意して使えれば,三角比の相互関係はばっちり!
三角比の相互関係
$$\tan\theta=\frac{\sin\theta}{\cos\theta}$$
$$\sin^2\theta+\cos^2\theta=1$$
$$ 1+\tan^2\theta=\frac{1}{\cos^2\theta}$$
ただし $(\sin\theta)^2=\sin^2\theta$,$(\cos\theta)^2=\cos^2\theta$,$(\tan\theta)^2=\tan^2\theta$

これを覚えよう!
三角比の相互関係の証明
三角比の定義
$$\sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r},\tan\theta=\frac{y}{x}$$
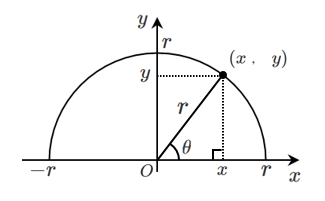
詳しい三角比の定義はこれ↓

$\tan\theta=\frac{\sin\theta}{\cos\theta}$ の証明
$\displaystyle{\sin\theta=\frac{y}{r}}$,$\displaystyle{\cos\theta=\frac{x}{r}}$ より $y=r\sin\theta$,$x=r\cos\theta$
$\displaystyle{\tan\theta=\frac{y}{x}=\frac{r\sin\theta}{r\cos\theta}=\frac{\sin\theta}{\cos\theta}}$
よって $\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}$
$\sin^2\theta+\cos^2\theta=1$ の証明
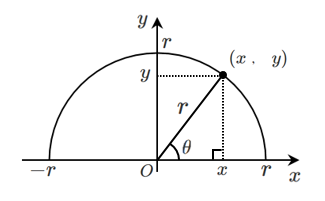
三平方の定理より $x^2+y^2=r^2$
$y=r\sin\theta$,$x=r\cos\theta$ を代入して
$r^2(\cos\theta)^2+r^2(\sin\theta)^2=r^2$
両辺を $r^2$ でわると
$\sin^2\theta+\cos^2\theta=1$
$ 1+\tan^2\theta=\frac{1}{\cos^2\theta}$
$\sin^2\theta+\cos^2\theta=1$ の両辺を $\cos^2\theta$ でわると
$$\displaystyle{\frac{\sin^2\theta}{\cos^2\theta}+1=\frac{1}{\cos^2\theta}}$$
$$\displaystyle{1+\left(\frac{\sin\theta}{\cos\theta}\right)^2=\frac{1}{\cos^2\theta}}$$
$$\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}$$
三角比の相互関係の使い方
● $\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}$
$\sin\theta$,$\cos\theta$,$\tan\theta$ の中の2つが分かれば残りの1つが求まる
● $\sin^2\theta+\cos^2\theta=1$
$\sin\theta$,$\cos\theta$ の一方が分かれば他方が求まる
● $\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}$
$\tan\theta$,$\cos\theta$ の一方が分かれば他方が求まる
$\theta$ が鋭角か鈍角かには注意
$\theta$ が鋭角か鈍角かによって,$\cos\theta$ と $\tan\theta$ の符号が変わるので注意
| $\theta$ | 鋭角 | 鈍角 |
| $\sin\theta$ | $+$ | $+$ |
| $\cos\theta$ | $+$ | $-$ |
| $\tan\theta$ | $+$ | $-$ |
鋭角は $ 0^\circ<\theta<90^\circ$,鈍角は $ 90^\circ<\theta<180^\circ$
まとめ
● 三角比の相互関係
$$\tan\theta=\frac{\sin\theta}{\cos\theta}$$
$$\sin^2\theta+\cos^2\theta=1$$
$$1+\tan^2\theta=\frac{1}{\cos^2\theta}$$
● 三角比の相互関係の使い方
$\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}$ …… $\sin\theta$,$\cos\theta$,$\tan\theta$ の中の2つが分かれば残りの1つが求まる
$\sin^2\theta+\cos^2\theta=1$ …… $\sin\theta$,$\cos\theta$ の一方が分かれば他方が求まる
$\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}$ …… $\tan\theta$,$\cos\theta$ の一方が分かれば他方が求まる
● $\theta$ は鋭角か鈍角か
| $\theta$ | 鋭角 | 鈍角 |
| $\sin\theta$ | $+$ | $+$ |
| $\cos\theta$ | $+$ | $-$ |
| $\tan\theta$ | $+$ | $-$ |
鋭角は $ 0^\circ<\theta<90^\circ$,鈍角は $ 90^\circ<\theta<180^\circ$
$\sin\theta$ は $\theta$ が鋭角でも鈍角でも正
$\cos\theta$,$\tan\theta$ は $\theta$ が鋭角なら正,鈍角なら負
問題
(1) $\theta$ が鈍角とする。$\displaystyle{\sin\theta=\frac{2}{3}}$ のとき,$\cos\theta$ と $\tan\theta$ の値を求めよ。
(2) $\theta$ が鋭角とする。$\displaystyle{\tan\theta=\frac{3}{4}}$ のとき,$\sin\theta$ と $\cos\theta$ の値を求めよ。
解答
(1) $\theta$ が鈍角とする。$\displaystyle{\sin\theta=\frac{2}{3}}$ のとき,$\cos\theta$ と $\tan\theta$ の値を求めよ。
$\sin^2\theta+\cos^2\theta=1$ より ($\sin\theta$ が与えられているので $\cos\theta$ が求まる)
\begin{eqnarray} \cos^2\theta &=& 1-\sin^2\theta \\\\ &=& 1-\left(\frac{2}{3}\right)^2 \\\\ &=& \frac{5}{9} \end{eqnarray}$\theta$ は鈍角なので $\cos\theta<0$ より
$\displaystyle{\cos\theta=-\frac{\sqrt{5}}{3}}$
$\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}$ より ($\sin\theta$ と $\cos\theta$ があるので $\tan\theta$ が求まる)
$$\displaystyle{\tan\theta=\frac{\frac{2}{3}}{-\frac{\sqrt{5}}{3}}=-\frac{2}{\sqrt{5}}}$$
(2) $\theta$ が鋭角とする。$\displaystyle{\tan\theta=\frac{3}{4}}$ のとき,$\sin\theta$ と $\cos\theta$ の値を求めよ。
$\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}$ より ($\tan\theta$ が与えられているので $\cos\theta$ が求まる)
\begin{eqnarray} 1+\left(\frac{3}{4}\right)^2 &=& \frac{1}{\cos^2\theta} \\\\ \frac{1}{\cos^2\theta} &=& \frac{25}{16}\\\\ \cos^2\theta &=& \frac{16}{25} \end{eqnarray}$\theta$ が鋭角なので $\cos\theta>0$ より
$\displaystyle{\cos\theta=\frac{4}{5}}$
$\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}$ より ($\cos\theta$ と $\tan\theta$ があるので $\sin\theta$ が求まる)
$$\sin\theta=\tan\theta\cos\theta=\frac{3}{4}×\frac{4}{5}=\frac{3}{5}$$

3つの式を使いこなせるように練習しよう!
特に,$\sin^2\theta+\cos^2\theta=1$ は使う機会が多いよ!

あとは鋭角か鈍角か注意しないといけないね!




コメント