高校数学Ⅱの【三角関数】で学ぶ『三角関数のグラフの拡大・縮小と平行移動』について解説!
拡大・縮小について2種類,平行移動について2種類
を理解すれば完璧です!
この投稿を見れば,三角関数の式とグラフの関係はバッチリ!
三角関数のグラフの拡大・縮小と平行移動のパターン
$y=\sin\theta$ のグラフに対して
(ア) $y=a\sin\theta$ ➡ $y$ 軸方向に $a$ 倍に拡大(縮小)
(イ) $y=\sin k\theta$ ➡ $\theta$ 軸方向に $\displaystyle{\frac{1}{k}}$ 倍に拡大(縮小)
(ウ) $y=\sin\theta+q$ ➡ $y$ 軸方向に $q$ だけ平行移動
(エ) $y=\sin(\theta-p)$ ➡ $\theta$ 軸方向に $p$ だけ平行移動
(ア) 縦 の 拡大・縮小
(イ) 横 の 拡大・縮小
(ウ) 縦 の 平行移動
(エ) 横 の 平行移動
の4パターンを理解すれば完璧!
$y=a\sin\theta$(縦の拡大・縮小)
$y=\sin\theta$ のグラフに対して
(ア) $y=a\sin\theta$ ➡ $y$ 軸方向に $a$ 倍に拡大(縮小)
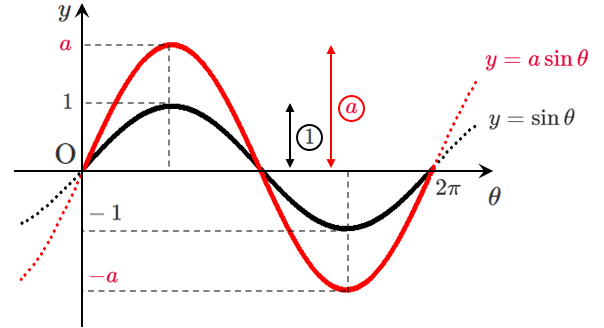
縦の拡大・縮小なので
周期は変わらず $2\pi$ である
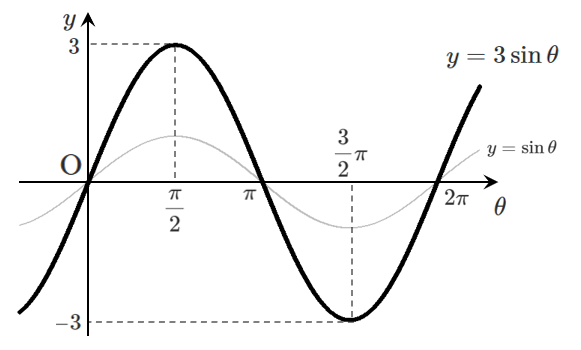
$y=3\sin\theta$ のグラフは,$y=\sin\theta$ のグラフを $y$ 軸方向に $3$ 倍拡大した曲線
よって,周期は $2\pi$
$y=\sin k\theta$(横の拡大・縮小)
$y=\sin\theta$ のグラフに対して
(イ) $y=\sin k\theta$ ➡ $\theta$ 軸方向に $\displaystyle{\frac{1}{k}}$ 倍に拡大(縮小)
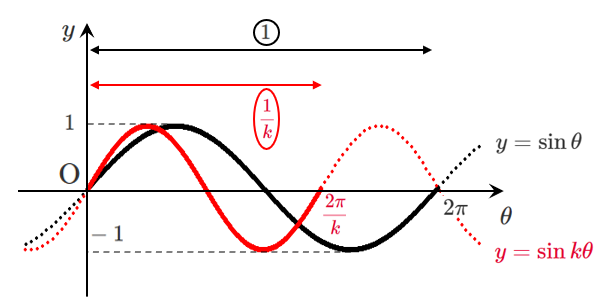
$y=\sin\theta$ の周期 $2\pi$ に対して,
$y=\sin k\theta$ の周期は $\displaystyle{\frac{1}{k}}$ 倍(逆数倍)されるので
$y=\sin k\theta$ の周期は $\displaystyle{\frac{2\pi}{k}}$ である

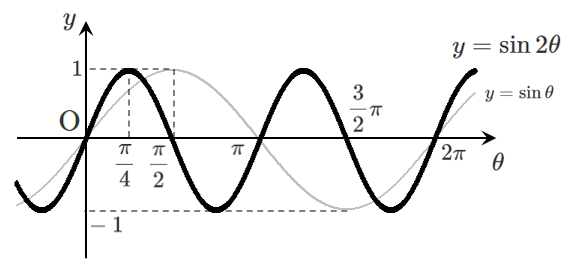
(1) $y=\sin 2\theta$ (2) $y=\sin 3\theta$ (3) $\displaystyle{y=\sin\frac{\theta}{2}}$
(1) $y=\sin 2\theta$ のグラフは,$y=\sin\theta$ のグラフを $\theta$ 軸方向に $\displaystyle{\frac{1}{2}}$ 倍に縮小した曲線
周期は $\displaystyle{\frac{1}{2}}$ 倍されるので $\displaystyle{2\pi\times\frac{1}{2}=\pi}$
よって,$y=\sin2\theta$ の周期は $\pi$
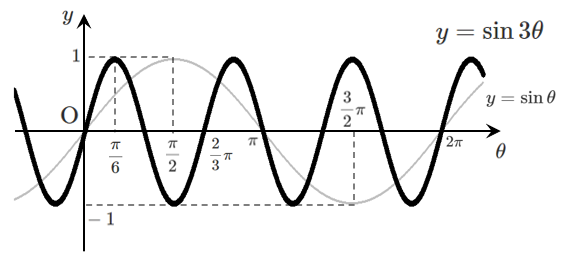
(2) $y=\sin3\theta$ のグラフは,$y=\sin\theta$ のグラフを $\theta$ 軸方向に $\displaystyle{\frac{1}{3}}$ 倍に縮小した曲線
周期は $\displaystyle{\frac{1}{3}}$ 倍されるので $\displaystyle{2\pi\times\frac{1}{3}=\frac{2}{3}\pi}$
よって,$y=\sin3\theta$ の周期は $\displaystyle{\frac{2}{3}\pi}$
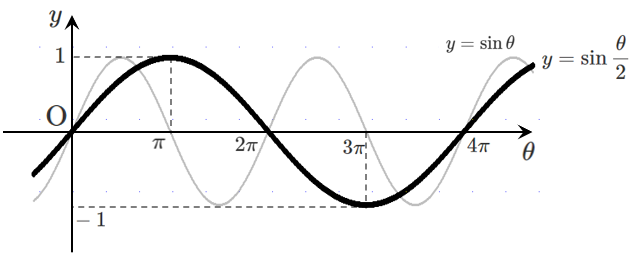
(3) $\displaystyle{y=\sin\frac{\theta}{2}}$ のグラフは,$y=\sin\theta$ のグラフを $\theta$ 軸方向に $2$ 倍拡大した曲線
周期は $2$ 倍されるので $2\pi\times2=4\pi$
よって,$\displaystyle{y=\sin\frac{\theta}{2}}$ の周期は $4\pi$
$y=\sin\theta+q$(縦の平行移動)
$y=\sin\theta$ のグラフに対して
(ウ) $y=\sin\theta+q$ ➡ $y$ 軸方向に $q$ だけ平行移動
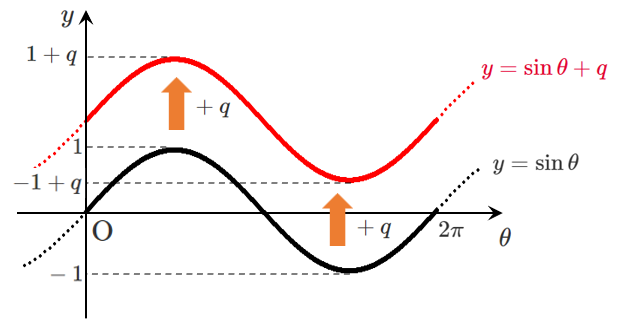
縦の平行移動なので
周期は変わらず $2\pi$ である
2 次関数 $y=x^2+1$ が $y=x^2$ を $y$ 軸方向に $1$ だけ平行移動したグラフ
であることと同様
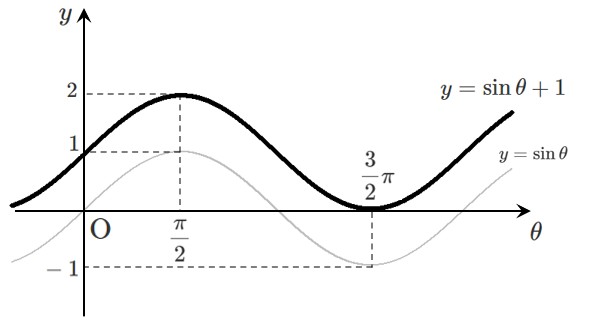
$y=\sin\theta+1$ のグラフは,$y=\sin\theta$ のグラフを $y$ 軸方向に $1$ だけ平行移動した曲線
よって,周期は $2\pi$
$y=\sin(\theta-p)$(横の平行移動)
$y=\sin\theta$ のグラフに対して
(エ) $y=\sin(\theta-p)$ ➡ $\theta$ 軸方向に $p$ だけ平行移動
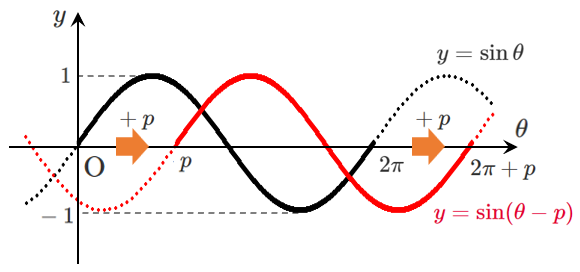
横の平行移動なので
周期は変わらず $2\pi$ である
2 次関数 $y=(x-1)^2$ が $y=x^2$ を $x$ 軸方向に $1$ だけ平行移動したグラフ
であることと同様
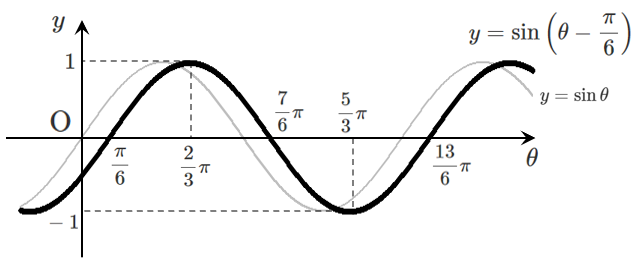
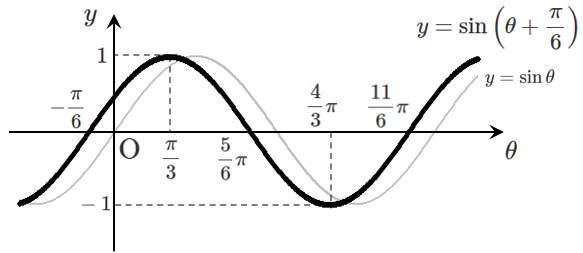
(1) $\displaystyle{y=\sin\left(\theta-\frac{\pi}{6}\right)}$ (2) $\displaystyle{y=\sin\left(\theta+\frac{\pi}{6}\right)}$
(1) $\displaystyle{y=\sin\left(\theta-\frac{\pi}{6}\right)}$ のグラフは,$y=\sin\theta$ のグラフを $\theta$ 軸方向に $\displaystyle{\frac{\pi}{6}}$ だけ平行移動した曲線
よって,周期は $2\pi$
(2) $\displaystyle{y=\sin\left(\theta+\frac{\pi}{6}\right)}$ のグラフは,$y=\sin\theta$ のグラフを $\theta$ 軸方向に $\displaystyle{-\frac{\pi}{6}}$ だけ平行移動した曲線
よって,周期は $2\pi$
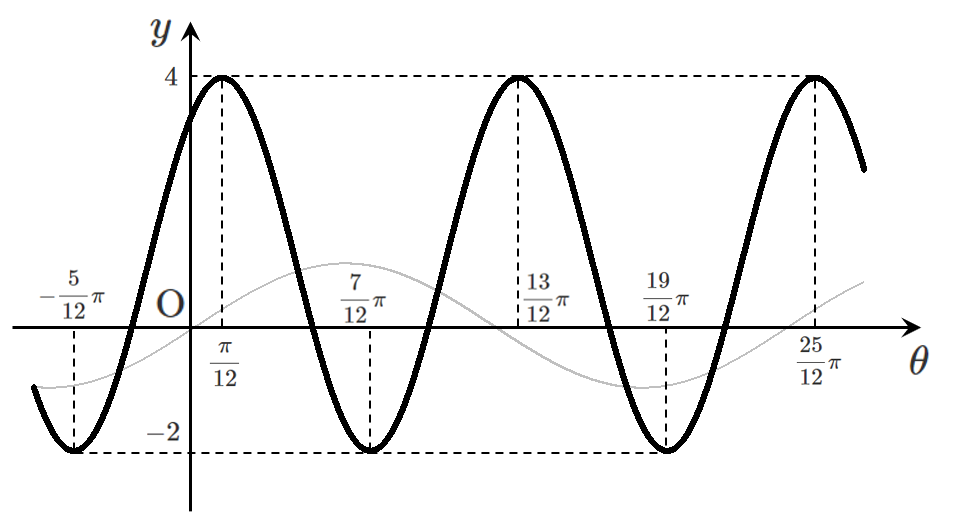
$y=a\sin k(\theta-p)+q$ のグラフ
$y=\displaystyle{3\sin\left(2\theta+\frac{\pi}{3}\right)+1=3\sin2\left(\theta+\frac{\pi}{6}\right)+1}$
このグラフは,$y=\sin\theta$ のグラフを
$y$ 軸方向に $3$ 倍に拡大,
$\theta$ 軸方向に $\displaystyle{\frac{1}{2}}$ 倍に縮小
した後,
$y$ 軸方向に $1$ だけ平行移動し,
$\theta$ 軸方向に $\displaystyle{-\frac{\pi}{6}}$ だけ平行移動した曲線


よって,周期は $\displaystyle{2\pi\times\frac{1}{2}=\pi}$ である




コメント