高校数学Ⅱの【三角関数】で学ぶ『三角関数の合成』について解説!
『三角関数の合成』は,模試頻出のテーマ!
三角関数の合成の手順,三角関数の合成とは何かについて確実に理解することが重要!
この投稿を見れば,『三角関数の合成』の基本はバッチリ!
加法定理と合成の関係

「三角関数の合成」とは何か?
「加法定理」から学ぼう!
正弦の加法定理
$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$
を用いると
$\displaystyle{2\sin\left(\theta+\frac{\pi}{3}\right)=2\left(\sin\theta\cos\frac{\pi}{3}+\cos\theta\sin\frac{\pi}{3}\right)}$
$\displaystyle{=2\left(\frac{1}{2}\sin\theta+\frac{\sqrt{3}}{2}\cos\theta\right)}$
$\displaystyle{=\sin\theta+\sqrt{3}\cos\theta}$
つまり
$\displaystyle{2\sin\left(\theta+\frac{\pi}{3}\right)=\sin\theta+\sqrt{3}\cos\theta}$
が成り立つ
よって
$\displaystyle{2\sin\left(\theta+\frac{\pi}{3}\right)}$ は「加法定理」を用いれば, $\displaystyle{\sin\theta+\sqrt{3}\cos\theta}$ に式変形できる
逆に
$\displaystyle{\sin\theta+\sqrt{3}\cos\theta}$ を $\displaystyle{2\sin\left(\theta+\frac{\pi}{3}\right)}$ に式変形することを「三角関数の合成」という
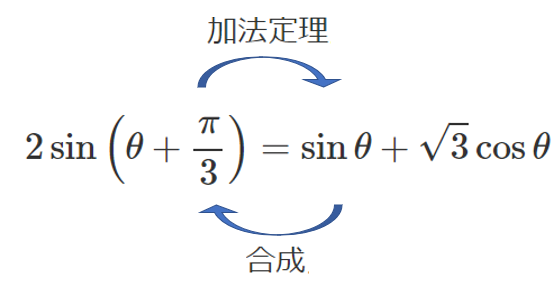

計算でみると,「加法定理」と逆の計算が「合成」だね!
三角関数の合成

「三角関数の合成」のやり方を学ぼう!
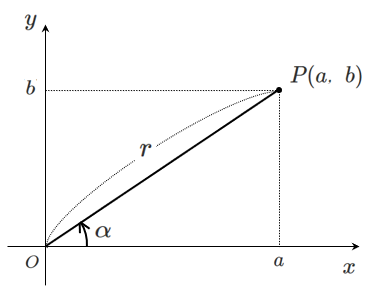
下図のように,座標が $(a,b)$ である点 $P$ をとる
$x$ 軸の正の部分から線分 $OP$ まで測った角を $\alpha$ とし,$OP=r$ とする
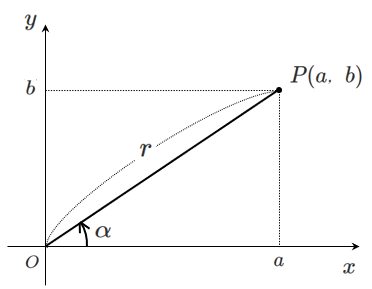
三角関数の定義より
$\displaystyle{\cos\alpha=\frac{a}{r},\sin\alpha=\frac{b}{r}}$
式変形すると
$a=r\sin\alpha,b=r\sin\alpha$
よって
$a$$\sin\theta+$$b$$\cos\theta=$$r\cos\alpha$$\sin\theta+$$r\sin\alpha$$\cos\theta$
$=r($$\sin\theta\cos\alpha+\cos\theta\sin\alpha$$)$
$=r$$\sin(\theta+\alpha)$
以上より,三角関数の合成は
$a\sin\theta+b\cos\theta=r\sin(\theta+\alpha)$
つまり,$a\sin\theta+b\cos\theta$ を合成するなら
① 点 $(a,b)$ をとる
② $r$ と $\alpha$ を求める
③ $r\sin(\theta+\alpha)$ と変形する
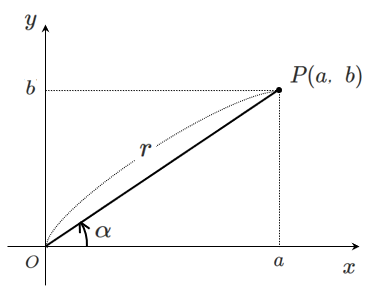
ここで, $r=\sqrt{a^2+b^2}$ より
$a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin(\theta+\alpha)$
とすると,以下のようにまとめられる
$a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin(\theta+\alpha)$
ただし,$\displaystyle{\cos\alpha=\frac{a}{\sqrt{a^2+b^2}},\sin\alpha=\frac{b}{\sqrt{a^2+b^2}}}$
三角関数の合成の手順

「三角関数の合成」の手順をまとめるとこれ!
$a\sin\theta+b\cos\theta$ の合成
- 点 $(a,b)$ をとる
- $r$ と $\alpha$ を求める
- $r\sin(\theta+\alpha)$ に式変形する

問題

問題を解いてみよう!
次の式を $r\sin(\theta+\alpha)$ の形に表せ。
(1) $\sin\theta+\sqrt{3}\cos\theta$
(2) $\sin\theta+\cos\theta$
(3) $\sqrt{3}\sin\theta-\cos\theta$
(1) $\sin\theta+\sqrt{3}\cos\theta$

$\displaystyle{\sin\theta+\sqrt{3}\cos\theta=2\sin\left(\theta+\frac{\pi}{3}\right)}$
(2) $\sin\theta+\cos\theta$
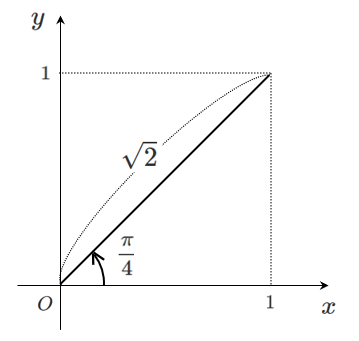
$\displaystyle{\sin\theta+\cos\theta=\sqrt{2}\sin\left(\theta+\frac{\pi}{4}\right)}$
(3) $\sqrt{3}\sin\theta-\cos\theta$
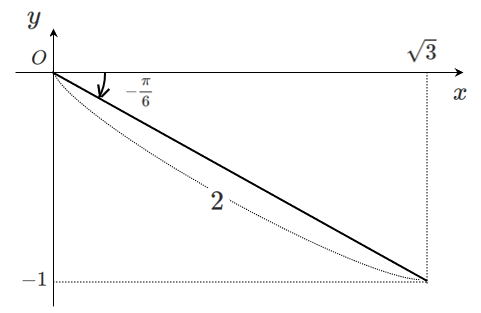
$\displaystyle{\sqrt{3}\sin\theta-\cos\theta=2\sin\left(\theta-\frac{\pi}{6}\right)}$
<別解>
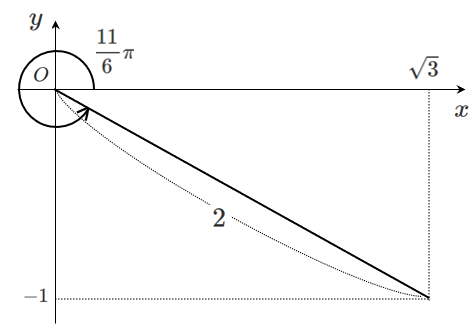
$\displaystyle{\sqrt{3}\sin\theta-\cos\theta=2\sin\left(\theta+\frac{11}{6}\pi\right)}$

このように,合成の表し方は1通りではなく,何通りも存在するよ!
でも,問題の書き方によっては,答えが1通りになるので注意!

どういう問題の書き方だったら,答えが1通りになるの?

以下の問題をみてみよう!
ただし,$r>0$,$-\pi<\alpha<\pi$ とする。
○ $\displaystyle{\sqrt{3}\sin\theta-\cos\theta=2\sin\left(\theta-\frac{\pi}{6}\right)}$
× $\displaystyle{\sqrt{3}\sin\theta-\cos\theta=2\sin\left(\theta+\frac{11}{6}\pi\right)}$
$\displaystyle{\alpha=\frac{11}{6}\pi}$ が $-\pi<\alpha<\pi$ を満たしていないため

問題文をよく読まないといけないね!
$\alpha$ が求まらない場合

$\alpha$ が求まる問題ばかりではない!
$\alpha$ が求まらない場合の解き方を学ぼう!
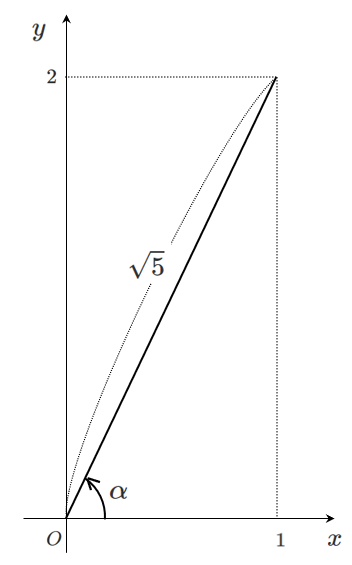
$\sin\theta+2\cos\theta=\sqrt{5}\sin(\theta+\alpha)$
ただし,$\displaystyle{\sin\alpha=\frac{2}{\sqrt{5}},\cos\alpha=\frac{1}{\sqrt{5}}}$

$\alpha$ の角自体は求まらないので,$\sin\alpha$ と $\cos\alpha$ の値を求めておく!
cos の合成
三角関数の合成は,「sinの合成」が基本ですが,「cosの合成」もできます!
三角関数の合成は,加法定理と逆の計算なので,cosの加法定理の逆の計算をすれば,「cosの合成」ができます!
cosの加法定理
$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$
$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$
を利用する
次の式を $r\cos(\theta+\alpha)$ の形に表せ。ただし,$r>0$,$-\pi<\alpha<\pi$ とする。
(1) $\sin\theta+\sqrt{3}\cos\theta$
(2) $\sin\theta+\cos\theta$
(3) $-\sqrt{3}\sin\theta+\cos\theta$
(1) $\sin\theta+\sqrt{3}\cos\theta$
$=\sqrt{3}\cos\theta+\sin\theta$
$\displaystyle{=2\left(\frac{\sqrt{3}}{2}\cos\theta+\frac{1}{2}\sin\theta\right)}$
$\displaystyle{=2\left(\cos\theta\cos\frac{\pi}{6}+\sin\theta\sin\frac{\pi}{6}\right)}$
$\displaystyle{=2\cos\left(\theta-\frac{\pi}{6}\right)}$
(2) $\sin\theta+\cos\theta$
$=\cos\theta+\sin\theta$
$\displaystyle{=\sqrt{2}\left(\frac{1}{\sqrt{2}}\cos\theta+\frac{1}{\sqrt{2}}\sin\theta\right)}$
$\displaystyle{=\sqrt{2}\left(\cos\theta\cos\frac{\pi}{4}+\sin\theta\sin\frac{\pi}{4}\right)}$
$\displaystyle{=\sqrt{2}\cos\left(\theta-\frac{\pi}{4}\right)}$
(3) $-\sqrt{3}\sin\theta+\cos\theta$
$=\cos\theta-\sqrt{3}\sin\theta$
$\displaystyle{=2\left(\frac{1}{2}\cos\theta-\frac{\sqrt{3}}{2}\sin\theta\right)}$
$\displaystyle{=2\left(\cos\theta\cos\frac{\pi}{3}-\sin\theta\sin\frac{\pi}{3}\right)}$
$\displaystyle{=2\cos\left(\theta+\frac{\pi}{3}\right)}$
まとめ
● 三角関数の合成
$a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin(\theta+\alpha)$
ただし,$\displaystyle{\cos\alpha=\frac{a}{\sqrt{a^2+b^2}},\sin\alpha=\frac{b}{\sqrt{a^2+b^2}}}$
● 三角関数の合成の手順
$a\sin\theta+b\cos\theta$ の合成
- 点 $(a,b)$ をとる
- $r$ と $\alpha$ を求める
- $r\sin(\theta+\alpha)$ に式変形する

よく出題されるので,きちんと解けるようにしておこう!




コメント