高校数学Ⅱの【三角関数】で学ぶ『三角関数の性質』について解説!
苦手な人が多い『三角関数の性質』に関する公式を徹底解説!
単位円で考えるとスッキリ理解することができます!
この投稿を見れば,『三角関数の性質』はバッチリ!
$\theta+2n\pi$ の公式
$n$ を整数とすると
$\sin(\theta+2n\pi)=\sin\theta$
$\cos(\theta+2n\pi)=\cos\theta$
$\tan(\theta+2n\pi)=\tan\theta$
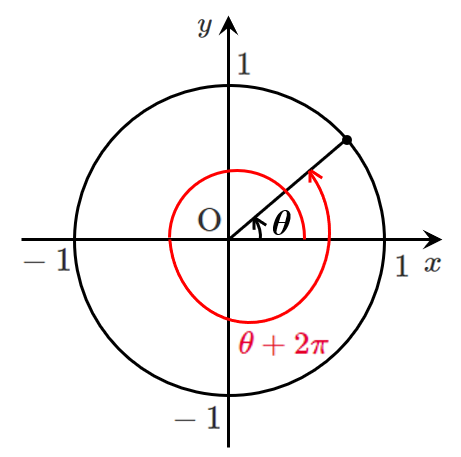
上図のように,動径は $2\pi$ で一周するので,
$\theta+2\pi$ の動径は $\theta$ の動径と同じ位置になる。
同様に,$\theta+2\pi\times2$,$\theta+2\pi\times3$,… の動径
$\theta+2\pi\times(-1)$,$\theta+2\pi\times(-2)$,… の動径
も $\theta$ の動径と同じ位置になる。
よって,$\theta+2\pi\times(整数)$ の動径は,$\theta$ の動径と同じ位置になるので,
整数 $n$ とすると,$\theta+2n\pi$ の動径は $\theta$ の動径と同じ位置になる。
$-\theta$ の公式
$\sin(-\theta)=-\sin\theta$
$\cos(-\theta)=\cos\theta$
$\tan(-\theta)=-\tan\theta$
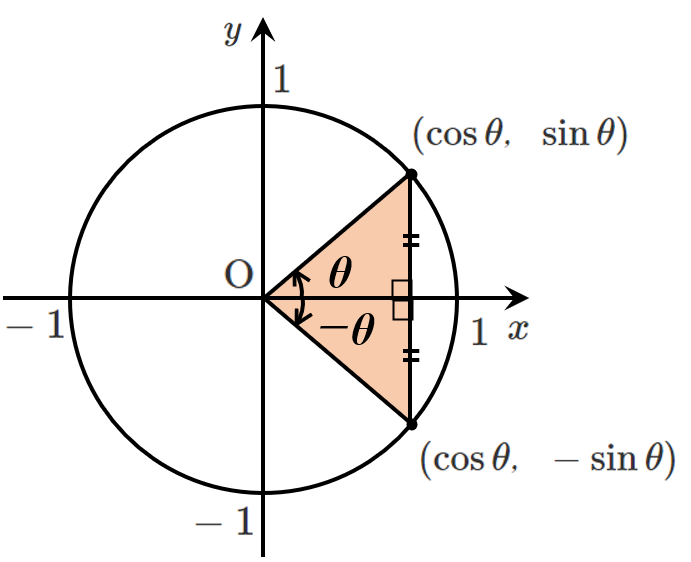
$y$ 座標は符号が異なるので $\sin(-\theta)=-\sin\theta$
$x$ 座標は等しいので $\cos(-\theta)=\cos\theta$
$\displaystyle{\tan(-\theta)=\frac{\sin(-\theta)}{\cos(-\theta)}=\frac{-\sin\theta}{\cos\theta}=-\tan\theta}$
$\pi-\theta$ の公式
$\sin(\pi-\theta)=\sin\theta$
$\cos(\pi-\theta)=-\cos\theta$
$\tan(\pi-\theta)=-\tan\theta$
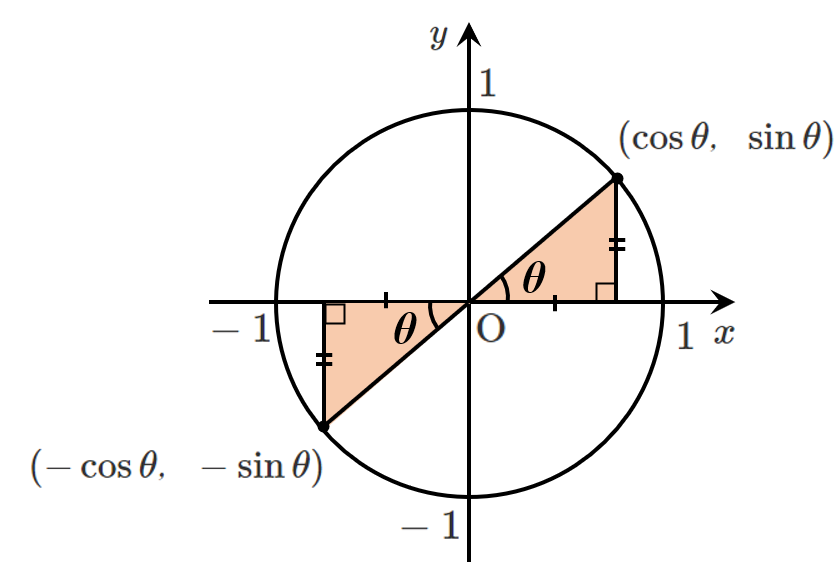
$y$ 座標は等しいので $\sin(\pi-\theta)=-\sin\theta$
$x$ 座標は符号が異なるので $\cos(\pi-\theta)=\cos\theta$$\displaystyle{\tan(\pi-\theta)=\frac{\sin(\pi-\theta)}{\cos(\pi-\theta)}=\frac{\sin\theta}{-\cos\theta}=-\tan\theta}$
$\pi+\theta$ の公式
$\sin(\pi+\theta)=-\sin\theta$
$\cos(\pi+\theta)=-\cos\theta$
$\tan(\pi+\theta)=\tan\theta$
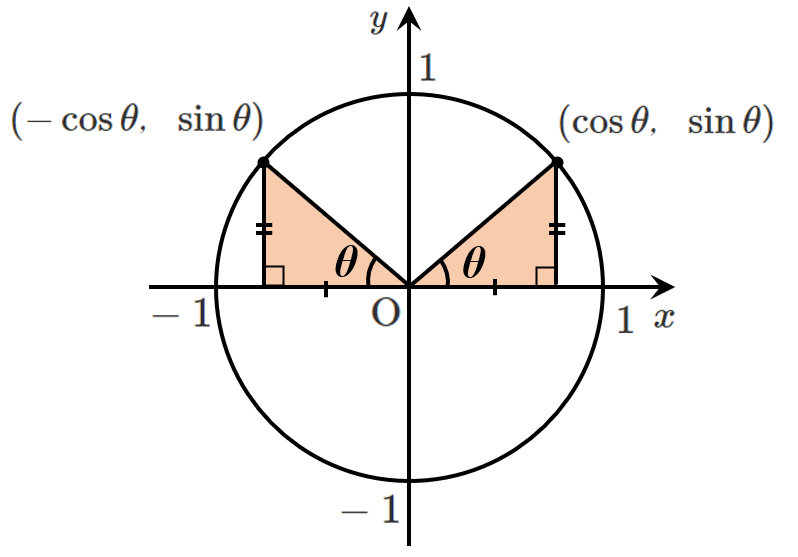
$y$ 座標は符号が異なるので $\sin(\pi+\theta)=-\sin\theta$
$x$ 座標は符号が異なるので $\cos(\pi+\theta)=-\cos\theta$
$\displaystyle{\tan(\pi+\theta)=\frac{\sin(\pi+\theta)}{\cos(\pi+\theta)}=\frac{-\sin\theta}{-\cos\theta}=\tan\theta}$
$\frac{\pi}{2}-\theta$ の公式
$\displaystyle{\sin\left(\frac{\pi}{2}-\theta\right)=\cos\theta}$
$\displaystyle{\cos\left(\frac{\pi}{2}-\theta\right)=\sin\theta}$
$\displaystyle{\tan\left(\frac{\pi}{2}-\theta\right)=\frac{1}{\tan\theta}}$
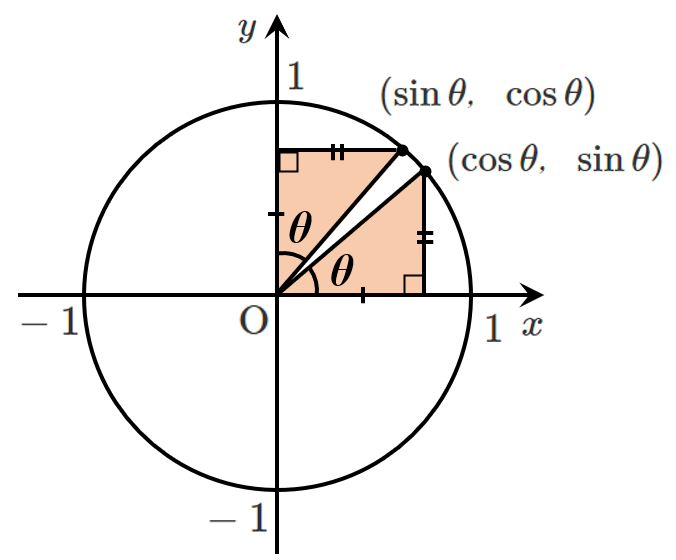
一方の $x$ 座標と他方の $y$ 座標が等しいので
$\displaystyle{\sin\left(\frac{\pi}{2}-\theta\right)=\cos\theta}$
$\displaystyle{\cos\left(\frac{\pi}{2}-\theta\right)=\sin\theta}$
$\displaystyle{\tan\left(\frac{\pi}{2}-\theta\right)=\frac{\sin\left(\frac{\pi}{2}-\theta\right)}{\cos\left(\frac{\pi}{2}-\theta\right)}=\frac{\cos\theta}{\sin\theta}=\frac{1}{\tan\theta}}$
$\frac{\pi}{2}+\theta$ の公式
$\displaystyle{\sin\left(\frac{\pi}{2}+\theta\right)=\cos\theta}$
$\displaystyle{\cos\left(\frac{\pi}{2}+\theta\right)=-\sin\theta}$
$\displaystyle{\tan\left(\frac{\pi}{2}+\theta\right)=-\frac{1}{\tan\theta}}$
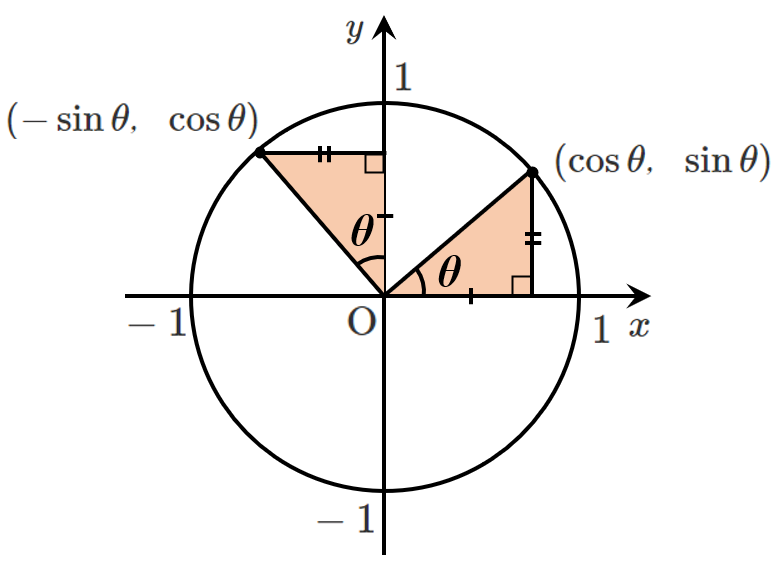
角 $\displaystyle{\frac{\pi}{2}+\theta}$ の $y$ 座標と角 $\theta$ の $x$ 座標が等しいので $\displaystyle{\sin\left(\frac{\pi}{2}+\theta\right)=\cos\theta}$
角 $\displaystyle{\frac{\pi}{2}+\theta}$ の $x$ 座標と角 $\theta$ の $y$ 座標の符号が異なるので $\displaystyle{\cos\left(\frac{\pi}{2}+\theta\right)=-\sin\theta}$
$\displaystyle{\tan\left(\frac{\pi}{2}+\theta\right)=\frac{\sin\left(\frac{\pi}{2}+\theta\right)}{\cos\left(\frac{\pi}{2}+\theta\right)}=\frac{\cos\theta}{-\sin\theta}=-\frac{1}{\tan\theta}}$
困ったら加法定理で計算
図を描いて思い出すのが重要ですが,
テストとかで困ったら『加法定理』で求まります!
加法定理はこれ↓
$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$
$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$
$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$
$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$
$\displaystyle{\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}}$
$\displaystyle{\tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}}$
加法定理の使い方の例
$\sin(\pi+\theta)=\sin\pi\cos\theta+\cos\pi\sin\theta$
$=0\cdot\cos\theta+(-1)\cdot\sin\theta$
$=-\sin\theta$
$\cos(\pi+\theta)=\cos\pi\cos\theta-\sin\pi\sin\theta$
$=(-1)\cdot\cos\theta-0\cdot\sin\theta$
$=-\cos\theta$
$\displaystyle{\tan(\pi+\theta)=\frac{\tan\pi+\tan\theta}{1-\tan\pi\tan\theta}}$
$\displaystyle{=\frac{0+\tan\theta}{1-0\cdot\tan\theta}}$
$=\tan\theta$

これで忘れても安心だね!




コメント