三角関数の相互関係

三角比の相互関係

ただし　$(\sin\theta)^2=\sin^2\theta$，$(\cos\theta)^2=\cos^2\theta$，$(\tan\theta)^2=\tan^2\theta$

三角比の相互関係の証明

三角関数の定義

$$\sin\theta=\frac{y}{r}，\cos\theta=\frac{x}{r}，\tan\theta=\frac{y}{x}$$

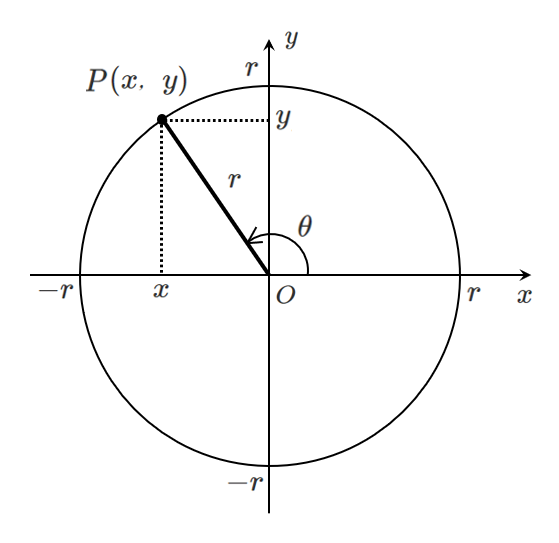
$\tan\theta=\frac{\sin\theta}{\cos\theta}$ の証明

　$\displaystyle{\sin\theta=\frac{y}{r}，\cos\theta=\frac{x}{r}}$ より，　　$y=r\sin\theta，x=r\cos\theta$

$\displaystyle{\tan\theta=\frac{y}{x}=\frac{r\sin\theta}{r\cos\theta}=\frac{\sin\theta}{\cos\theta}}$

　よって　　$\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}$

$\sin^2\theta+\cos^2\theta=1$ の証明

　三平方の定理より　$x^2+y^2=r^2$

　$y=r\sin\theta，x=r\cos\theta$ を代入して

$r^2(\cos\theta)^2+r^2(\sin\theta)^2=r^2$

　両辺を $r^2$ でわると

$\sin^2\theta+\cos^2\theta=1$

$ 1+\tan^2\theta=\frac{1}{\cos^2\theta}$

　$\sin^2\theta+\cos^2\theta=1$ の両辺を $\cos^2\theta$ でわると

$\displaystyle{\frac{\sin^2\theta}{\cos^2\theta}+1=\frac{1}{\cos^2\theta}}$

$\displaystyle{1+\left(\frac{\sin\theta}{\cos\theta}\right)^2=\frac{1}{\cos^2\theta}}$

$\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}$

三角関数の相互関係の使い方

● $\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}$

　$\sin\theta，\cos\theta，\tan\theta$ の中の２つが分かれば残りの１つが求まる

　

● $\sin^2\theta+\cos^2\theta=1$

　$\sin\theta，\cos\theta$ の一方が分かれば他方が求まる

　

● $\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}$

　$\tan\theta$，$\cos\theta$ の一方が分かれば他方が求まる

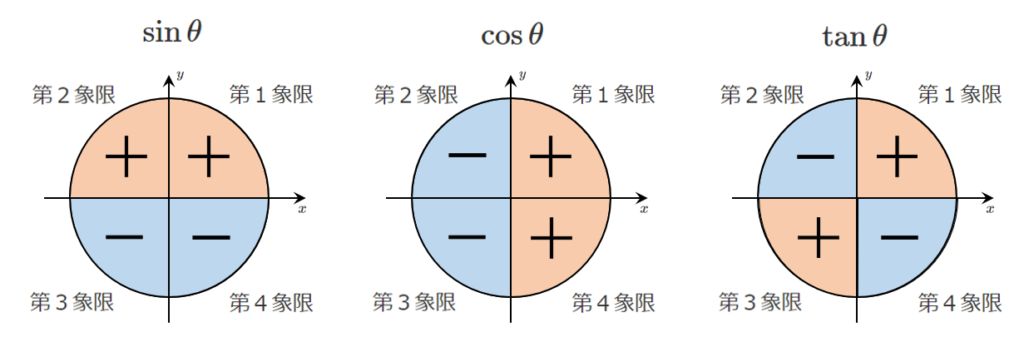
三角関数の符号

$\theta$ の動径が位置によって，$\sin\theta，\cos\theta，\tan\theta$ の符号が決まる

問題

(1)　$\theta$ の動径が第３象限にあり，$\displaystyle{\cos\theta=-\frac{4}{5}}$ のとき，$\sin\theta$ と $\tan\theta$

　　$\sin^2\theta+\cos^2\theta=1$ より　($\cos\theta$ が与えられているので $\sin\theta$ が求まる)

$\sin^2\theta=1-\cos^2\theta$

$\displaystyle{　　　　=1-\left(-\frac{4}{5}\right)^2}$

$\displaystyle{　　　=\frac{9}{25}}　　　　$

　　$\theta$ の動径が第３象限にあるので　　$\sin\theta<0$

　　よって　　　$\displaystyle{\cos\theta=-\frac{3}{5}}$

　　$\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}$ より　($\sin\theta$ と $\cos\theta$ があるので $\tan\theta$ が求まる)

$\displaystyle{\tan\theta=\frac{-\frac{3}{5}}{-\frac{4}{5}}=\frac{3}{4}}$

　

(2)　$\theta$ の動径が第４象限にあり，$\tan\theta=-2$ のとき，$\sin\theta$ と $\cos\theta$

　　$\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}$ より　($\tan\theta$ が与えられているので $\cos\theta$ が求まる)

$\displaystyle{1+(-2)^2=\frac{1}{\cos^2\theta}}$

$　\displaystyle{\frac{1}{\cos^2\theta}=5}$

$　\displaystyle{\cos^2\theta=\frac{1}{5}}$

　　$\theta$ の動径が第４象限にあるので　$\cos\theta>0$

　　よって　　$\displaystyle{\cos\theta=\frac{1}{\sqrt{5}}}$

　　$\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}$ より　($\cos\theta$ と $\tan\theta$ があるので $\sin\theta$ が求まる)

$\displaystyle{\sin\theta=\tan\theta\cos\theta=(-2)×\frac{1}{\sqrt{5}}=-\frac{2}{\sqrt{5}}}$

まとめ

● 三角関数の相互関係

$$\tan\theta=\frac{\sin\theta}{\cos\theta}$$

$$\sin^2\theta+\cos^2\theta=1$$

$$1+\tan^2\theta=\frac{1}{\cos^2\theta}$$

● 三角比の相互関係の使い方

　$\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}$　……　$\sin\theta$，$\cos\theta$，$\tan\theta$ の中の２つが分かれば残りの１つが求まる

　$\sin^2\theta+\cos^2\theta=1$　……　$\sin\theta$，$\cos\theta$ の一方が分かれば他方が求まる

　$\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}$　……　$\tan\theta$，$\cos\theta$ の一方が分かれば他方が求まる

● 三角関数の符号