不等式で表された集合

不等式で表された集合に関して，共通部分・和集合・補集合の考え方について分かりやすく解説しました！

数直線で問題を考えることで，とても簡単に理解することができます！

集合の表し方

集合の表し方には次の２つの方法があります。

例　$10$ 以下の正の偶数全体の集合を $A$ とする

① 要素を書き並べる方法

$A=\{2，4，6，8，10\}$

② 要素の条件を述べる方法

$A=\{$$x$$|$$x$ は $10$ 以下の正の偶数$\}$
　↑　　　　　↑　　　　
要素の代表　$x$ の満たす条件　

　他にも次のような表し方もできる

$A=\{2x|x$ は $5$ 以下の自然数$\}$

$A=\{2x|x=1，2，3，4，5\}$

要素が連続的な集合

$A=\{2，4，6，8，10\}$ のように，要素がとびとびの値（離散的な）集合は，「① 要素を書き並べる方法」が表しやすい。

しかし，「$1$ 以上 $2$ 以下の実数全体の集合 $B$」のように，要素が連続的な値をとる集合は，「② 要素の条件を述べる方法」の方が表しやすく，$B=\{x|1≦x≦2\}$ と表せる。

このように，要素が連続的な値をとる集合は，不等式で集合の条件を表す。

$B=\{1≦x≦2\}$ は誤りなので気を付けよう！

とても間違えやすいよ！

不等式で表された集合に関する問題

不等式で表された集合に関する問題は「数直線」を利用して考えよう！

　(1)　$A\cap B$　　$A$ と $B$ の共通部分

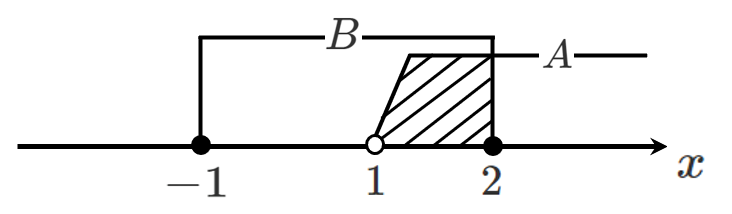
$A\cap B=\{x|1<x≦2\}$

　(2)　$A\cup B$　　$A$ と $B$ の和集合

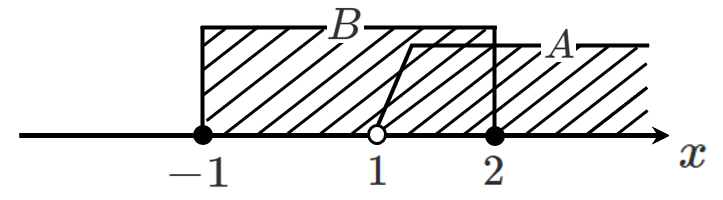
$A\cup B=\{x|-1≦x\}$

　(3)　$\overline{B}$　　$B$ の補集合

$\overline{B}=\{x|x<-1，2<x\}$

　(4)　$A\cap \overline{B}$　　$A$ と $\overline{B}$ の共通部分

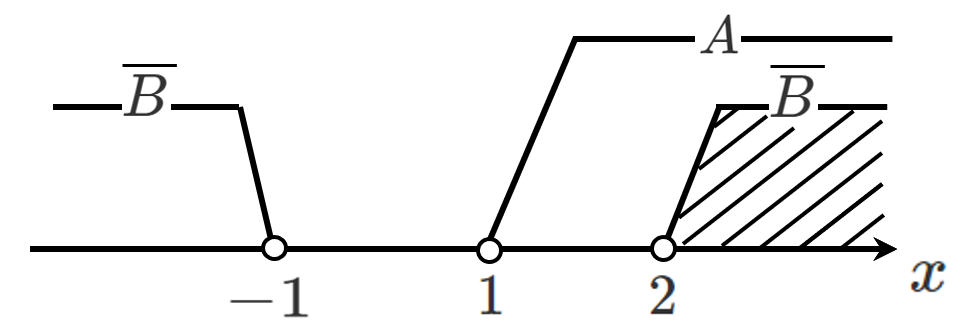
$A\cap \overline{B}=\{x|2<x\}$

　(5)　$\overline{A\cup B}$　　$A\cup B$ の補集合

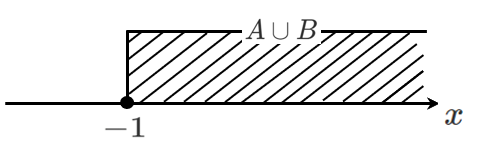
　　$A\cup B=\{x|-1≦x\}$ の補集合なので

$\overline{A\cup B}=\{x|x<-1\}$

🔰基本…まずはこの記事から！
🔵標準…基本問題や公式の理解度が重要！
🔴応用…場合分けなど思考力が要求される！