高校数学Ⅱで学ぶ『中心が原点でない円の接線の方程式』について解説!
中心が原点でない円の接線の方程式は、公式が複雑で覚えにくいので、
様々な解法アプローチを学ぶことが重要です!
この投稿を見れば、『中心が原点でない円の接線の方程式』はバッチリ!
原点を中心とする円の接線の方程式
円 $x^2+y^2=r^2$ 上の点 $(p,q)$ における接線の方程式は
$px+qy=r^2$
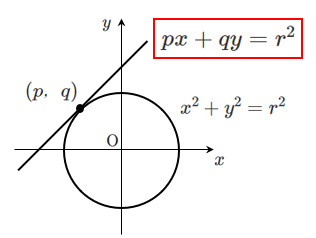
【参考:原点を中心とする円の接線】
中心が原点でない円の接線の方程式
円 $(x-a)^2+(y-b)^2=r^2$ 上の点 $(p,q)$ における接線の方程式は
$(p-a)(x-a)+(q-b)(y-b)=r^2$
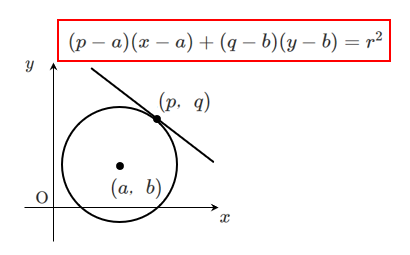
証明
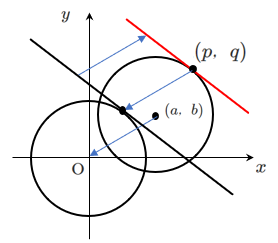
① 円 $(x-a)^2+(y-b)^2=r^2$ の中心が原点になるように,円と接点を $x$ 軸方向に $-a$,$y$ 軸方向に $-b$ だけ平行移動する
➡ 円の方程式は $x^2+y^2=r^2$,接点は $(p-a,q-b)$
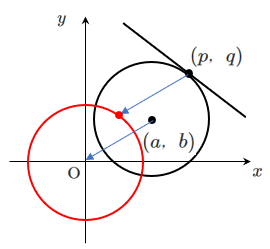
② 円の方程式は $x^2+y^2=r^2$ 上の点 $(p-a,q-b)$ における接線の方程式
➡ $(p-a)x+(q-b)y=r^2$ 【参考:原点を中心とする円の接線】
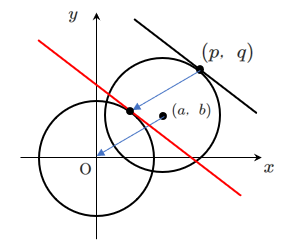
③ この接線を $x$ 軸方向に $a$,$y$ 軸方向に $b$ だけ平行移動する
➡ $(p-a)(x-a)+(q-b)(y-b)=r^2$ 【参考:平行移動と対称移動】
覚え方
一方の $x$,$y$ に接点 $p$,$q$ を代入する
➡ $(p-a)(x-a)+(q-b)(y-b)=r^2$
接点が与えられている問題
公式の利用
$(2-1)(x-1)+(6-3)(y-3)=10$ より $x+3y=20$
公式を忘れたとき
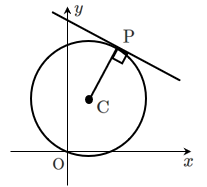
円の中心 $\textrm{C}(1,3)$ と円上の点 $\textrm{P}(2,6)$ を結ぶ線分 $\textrm{CP}$ の傾きは
$\displaystyle{\frac{6-3}{2-1}=3}$
求める接線は直線 $\textrm{CP}$ と垂直であるから,
接線の傾きは $\displaystyle{-\frac{1}{3}}$
よって,求める接線の方程式は
$\displaystyle{y-6=-\frac{1}{3}(x-2)}$
$\displaystyle{y=-\frac{1}{3}x+\frac{20}{3}}$
接点が与えられていない問題
(1) 傾きが $-3$ の接線
(2) 点 $(2,4)$ を通る接線
まずは,接線の方程式をおく
(1) $y$ 切片を $k$ として $y=-3x+k$
(2) 傾きを $m$ として $y-4=m(x-2)$
※ 傾きを文字でおく場合,$y$ 軸に平行な直線は表せないので,
「求める接線が $y$ 軸に平行な直線 $x=2$ でない」ことを記述しておく必要がある
円と直線が接する場合,「円の中心と直線の距離 $d$ と円の半径 $r$ が等しい」という式が作れる
(1) 求める接線の方程式を $y=-3x+k$ とおくと
円の中心と接線の距離と円の半径 $\sqrt{10}$ は等しいので
$\displaystyle{\frac{|3\cdot(-2)+1\cdot2-k|}{\sqrt{3^2+1^2}}=\sqrt{10}}$
$\displaystyle{\frac{|-k-4|}{\sqrt{10}}=\sqrt{10}}$ より $|k+4|=10$
$k+4=\pm10$ より $k=6,-14$
求める接線の方程式は $y=-3x+6$,$y=-3x-14$
(2) 直線 $x=2$ は接線ではないから,求める方程式を $y-4=m(x-2)$
すなわち $mx-y-2m+4=0$ とおくと
円の中心と接線の距離と円の半径 $\sqrt{10}$ は等しいので
$\displaystyle{\frac{|m\cdot(-2)-2-2m+4|}{\sqrt{m^2+(-1)^2}}=\sqrt{10}}$
$\displaystyle{\frac{|-4m+2|}{\sqrt{m^2+1}}=\sqrt{10}}$ より $|-4m+2|=\sqrt{10(m^2+1)}$
両辺を2乗すると $(-4m+2)^2=10(m^2+1)$
整理すると $3m^2-8m-3=0$
$(3m+1)(m-3)=0$
$\displaystyle{m=-\frac{1}{3},3}$
求める接線の方程式は $x+3y-14=0$,$3x-y-2=0$
接線の方程式をおいてから,
「円の方程式と接線の方程式で $y$ を消去した2次方程式の判別式 $D=0$」
という方法でも解くことができるが,
計算が煩雑になりやすいので注意!




コメント