
位置ベクトルとは何かについて学ぼう!
位置ベクトルとは
点 $A$ の位置ベクトルが $\vec{a}$ であることを
$A(\vec{a})$
と表す

点の位置がベクトルで表されていることがよくわからない…

位置ベクトルの概念は最初は分かりにくいね!
座標を参考にすると考えやすいよ!
座標の考え方
点 $A$ の座標が $(1,2)$ であることを
$A(1,2)$
と表す
座標というものは $x$ 軸と $y$ 軸が交わる原点 $O$ を基準として点が取られている
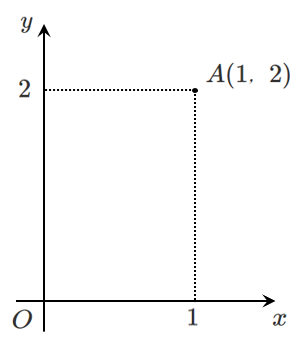
$A(1,2)$ は原点から $x$ 軸方向に $2$,$y$ 軸方向に $1$ だけ移動した点
原点を基準に座標をとって位置を考えていることがわかる

点 $A(○,○)$ と点 $A(\vec{A})$ は表現が似ているね!

座標 $(1,2)$ も位置ベクトル $\vec{a}$ も位置の情報を表すもの!
数学では,位置の情報を点の右側に書くよ!
位置ベクトルの考え方
点 $A$ の位置ベクトルが $\vec{a}$ であることを
$A(\vec{a})$
と表す
点 $A(\vec{a})$ も基準となる点 $O$ (どこにとってもよい)をつくることで,点 $A$ の位置がベクトルという形で可視化できる
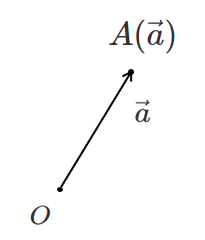
このとき,$\overrightarrow{OA}=\vec{a}$ と考える
ここに $B(\vec{b})$ という点が加わると
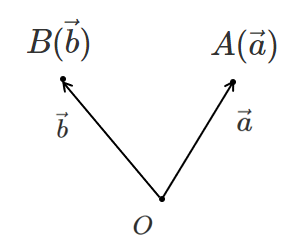
このとき,$\overrightarrow{OB}=\vec{b}$ と考える
位置ベクトルは,
基準となる点をとって,基準となる点からその位置に向かうベクトルによって位置を考える

基準となる点をとれば,ベクトルが作れるってことか!

その通り!
そのベクトルの向きや大きさで位置を把握できるね!
位置ベクトルの利用
2点を結ぶベクトル
2点 $A(\vec{a})$,$B(\vec{b})$ について
$\overrightarrow{AB}=\vec{b}-\vec{a}$
2点 $A(\vec{a})$,$B(\vec{b})$ について,$O$ を基準として考えると
$\overrightarrow{OA}=\vec{a}$, $\overrightarrow{OB}=\vec{b}$
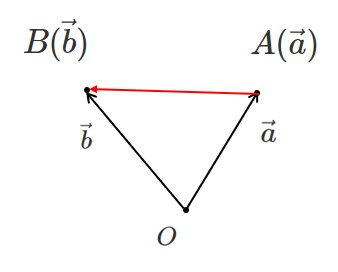
ベクトルの減法を用いると
$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$
すなわち
$\overrightarrow{AB}=\vec{b}-\vec{a}$

「後ー前」や「終点ー始点」と覚えておくと便利!
内分点と外分点の位置ベクトル
$A(\vec{a})$,$B(\vec{b})$ を結ぶ線分 $AB$ を $m:n$ に内分する点の位置ベクトルを $\vec{p}$,$m:n$ に外分する点の位置ベクトルを $\vec{q}$ とすると
$\displaystyle{\vec{p}=\frac{n\vec{a}+m\vec{b}}{m+n}}$
$\displaystyle{\vec{q}=\frac{-n\vec{a}+m\vec{b}}{m-n}}$

図形と方程式で習った内分点・外分点の座標と同じ考え方だよ!
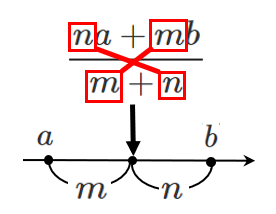
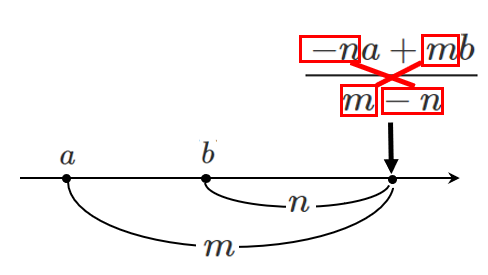
2点 $A(a)$,$B(b)$ に対して,線分 $AB$ を $m:n$ に内分する点 $P$ の座標 $p$ と $m:n$ に外分する点 $Q$ の座標 $q$は
$\displaystyle{p=\frac{na+mb}{m+n}}$
$\displaystyle{q=\frac{-na+mb}{m-n}}$
詳しくはこれ↓


基準となる点 $O$ を作れば,内分点と外分点におけるベクトルと考え方は同じ!
● 内分点におけるベクトル
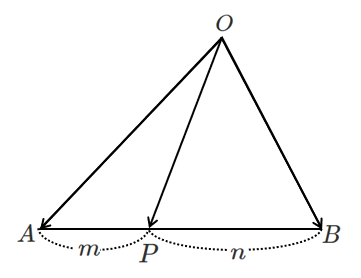
$\displaystyle{\overrightarrow{OP}=\frac{n\overrightarrow{OA}+m\overrightarrow{OB}}{m+n}}$
● 外分点におけるベクトル
$m>n$ のとき
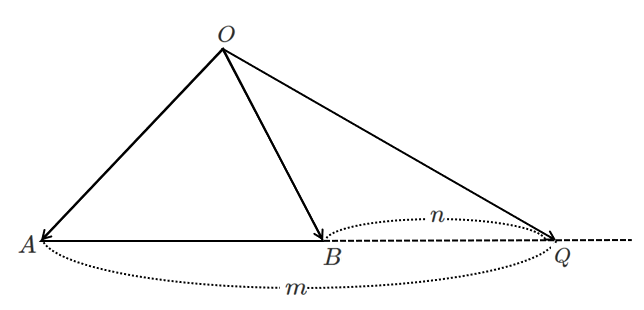
$m<n$ のとき
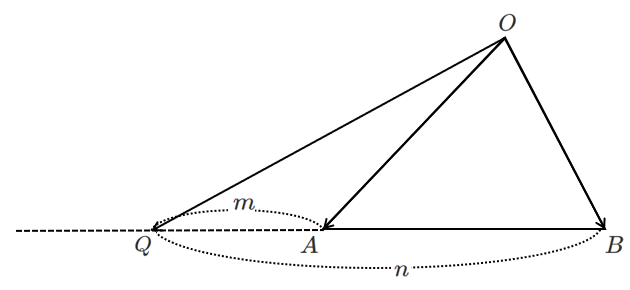
$\displaystyle{\overrightarrow{OQ}=\frac{-n\overrightarrow{OA}+m\overrightarrow{OB}}{m-n}}$

習った内容とつながるのがおもしろいね!
重心の位置ベクトル
$A(\vec{a})$,$B(\vec{b})$,$C(\vec{c})$ を頂点とする $\triangle ABC$ の重心 $G$ の位置ベクトル $\vec{g}$ は
$\displaystyle{\vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}}$

まずは重心について復習しよう!
中線 … 三角形の頂点とそれに向かい合う辺の中点を結ぶ線分
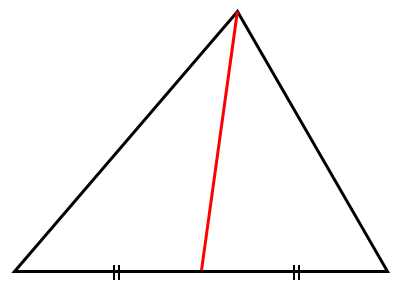
三角形について,中線を引くと
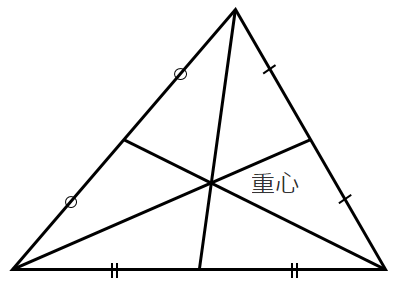
中線は1点で交わり,この交点を「重心」という
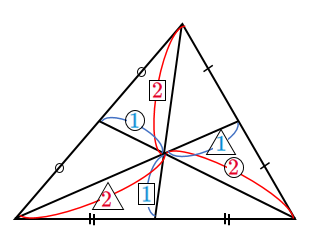
重心は各中線を $2:1$ に内分する
<証明>
$\triangle ABC$ において,辺 $BC$ の中点($1:1$ に内分する点)を $M(\vec{m})$ とすると
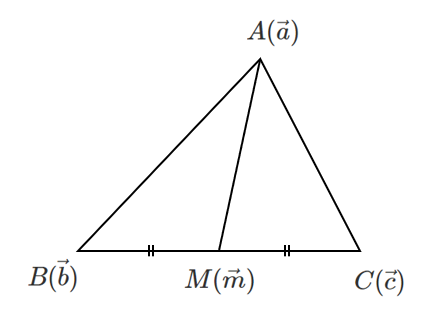
線分 $AM$ を $2:1$ に内分する点が $G(\vec{g})$ なので
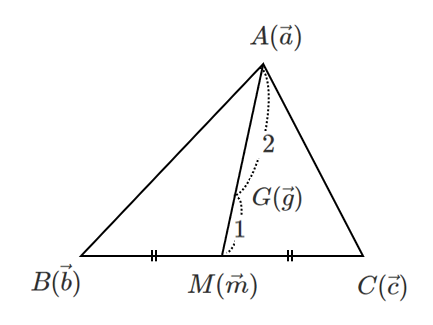

これも重心の座標と似ているね!
まとめ
● 位置ベクトル
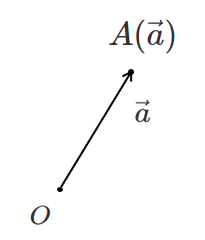
$\overrightarrow{OA}=\vec{a}$
● 2点を結ぶベクトル
2点 $A(\vec{a})$,$B(\vec{b})$ について
$\overrightarrow{AB}=\vec{b}-\vec{a}$
● 内分点と外分点の位置ベクトル
$A(\vec{a})$,$B(\vec{b})$ を結ぶ線分 $AB$ を $m:n$ に内分する点の位置ベクトルを $\vec{p}$,$m:n$ に外分する点の位置ベクトルを $\vec{q}$ とすると
$\displaystyle{\vec{p}=\frac{n\vec{a}+m\vec{b}}{m+n}}$
$\displaystyle{\vec{q}=\frac{-n\vec{a}+m\vec{b}}{m-n}}$
● 重心の位置ベクトル
$A(\vec{a})$,$B(\vec{b})$,$C(\vec{c})$ を頂点とする $\triangle ABC$ の重心 $G$ の位置ベクトル $\vec{g}$ は
$\displaystyle{\vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}}$

数学Ⅱの「図形と方程式」との関係性が分かってきたらばっちり!




コメント