余事象とは
事象 … 試行の結果として起こる事柄
$A$ の余事象 … 事象 $A$ が起こらないという事象
$A$ の余事象を $\overline{A}$ と表す
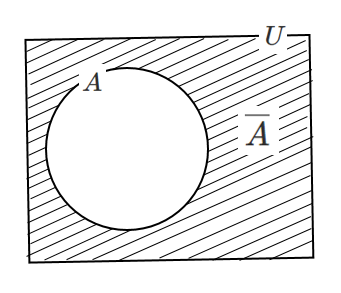

集合の補集合と似ているね!
集合の復習はこれ↓
余事象の確率の求め方

確率の全体は $1$ なので,$1$ から $A$ の確率を引くと $\overline{A}$ の確率が求まるよ!
「5の倍数でない数を引く」という事象は
「5の倍数を引く」という事象の余事象である
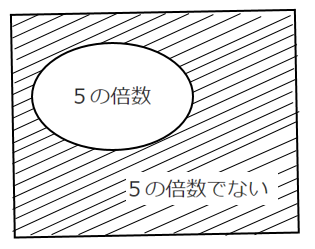
「5の倍数を引く」確率は $\displaystyle{\frac{10}{50}}$
「5の倍数でない数を引く」確率は
$1-(5 の倍数を引く確率)$ で求まるので
$\displaystyle{1-\frac{10}{50}=\frac{4}{5}}$

余事象を使わない解き方もあるよ!
この解き方でもOK!
【余事象を使わない解き方】
5の倍数でない数は $40$ 通り
5の倍数でない数を引く確率は
$\displaystyle{\frac{40}{50}=\frac{4}{5}}$
「少なくとも…」の問題は余事象を使う

余事象を使う問題でよく出題されるのが,「少なくとも…」という問題!
このキーワードがあったら,余事象を使って解けるようにしよう!
「少なくとも1枚が偶数である」という事象は
「3枚とも奇数である」という事象の余事象である
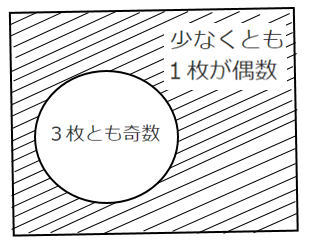
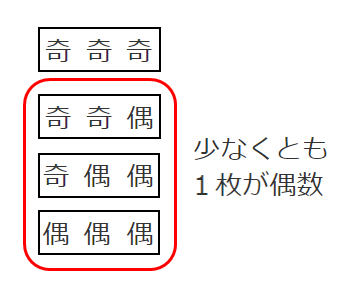
「3枚とも奇数である」確率は
$\displaystyle{\frac{_3C_3}{_6C_3}=\frac{1}{20}}$
「少なくとも1枚が偶数である」の確率は
$\displaystyle{1-\frac{1}{20}=\frac{19}{20}}$
「少なくとも…」の余事象は「少なくとも…」の否定を参考にしよう↓

組合せ $_nC_r$ を使った確率は↓

まとめ
● 余事象
事象 … 試行の結果として起こる事柄
$A$ の余事象 … 事象 $A$ が起こらないという事象
$A$ の余事象を $\overline{A}$ と表す
● 余事象の確率
$(\overline{A} の確率)=1-(A の確率)$
● 「少なくとも…」の確率
余事象を使って解く
問題
(1) $1~100$ の番号札から1枚を引くとき,3の倍数でない数を引く確率
(2) 赤玉4個と白玉3個入った袋から同時に3個取り出すとき,少なくとも1個は白玉である確率
(3) さいころを2個同時に投げるとき,異なる目が出る確率
(1) $1~100$ の番号札から1枚を引くとき,3の倍数でない数を引く確率
「3の倍数でない数を引く」という事象は
「3の倍数を引く」という事象の余事象である
「3の倍数を引く」確率は $\displaystyle{\frac{33}{100}}$
「3の倍数でない数を引く」確率は
$1-(3 の倍数を引く確率)$ で求まるので
$\displaystyle{1-\frac{33}{100}=\frac{67}{100}}$
(2) 赤玉4個と白玉3個入った袋から同時に3個取り出すとき,少なくとも1個は白玉である確率
「少なくとも1個は白玉である」という事象は
「3個とも赤玉である」という事象の余事象である
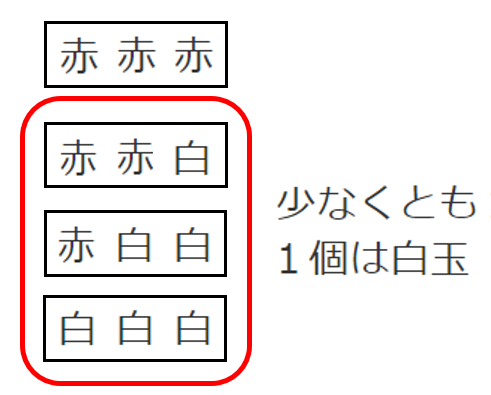
「3個とも赤玉である」確率は
$\displaystyle{\frac{_4C_3}{_7C_3}=\frac{4}{35}}$
「少なくとも1個は白玉である」確率は
$1-(3個とも赤玉である確率)$ で求まるので
$\displaystyle{1-\frac{4}{35}=\frac{31}{35}}$
(3) さいころを2個同時に投げるとき,異なる目が出る確率
「異なる目が出る」という事象は
「同じ目が出る」という事象の余事象である
「同じ目が出る」確率は
$\displaystyle{\frac{6}{36}=\frac{1}{6}}$
「異なる目が出る」確率は
$1-(同じ目が出る確率)$ で求まるので
$\displaystyle{1-\frac{1}{6}=\frac{5}{36}}$

余事象を上手に使って問題を解けるようにしよう!

特に,「少なくとも…」という問題は余事象を使えるようにしたいね!




コメント