ベクトルの内積
$\vec{a}$ と $\vec{b}$ のなす角を $\theta$ とすると
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$
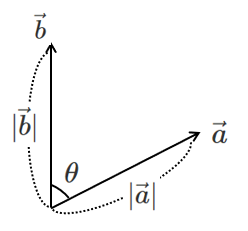
なす角 $\theta$ は「始点を合わせたときの角度」のこと
また,$0^\circ≦\theta≦180^\circ$

内積の基本はこれ↓


内積の性質
1 $\vec{a}\cdot\vec{a}=|\vec{a}|^2$
2 $\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}$
3 $(\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c}$
4 $\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}$
5 $(k\vec{a})\cdot\vec{b}=\vec{a}\cdot k\vec{b}=k(\vec{a}\cdot\vec{b})$ $k$ は定数
1 $\vec{a}\cdot\vec{a}=|\vec{a}|^2$
$\vec{a}$ と $\vec{a}$ のなす角は $0^\circ$
$\cos0^\circ=1$ なので
$\vec{a}\cdot\vec{a}=|\vec{a}||\vec{a}|\cos0^\circ=|\vec{a}|^2$
3 $(\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c}$
$\vec{a}=(a_1,a_2)$,$\vec{b}=(b_1,b_2)$,$\vec{c}=(c_1,c_2)$ とする
\begin{eqnarray} (\vec{a}+\vec{b})\cdot\vec{c} &=& (a_1+b_1)c_1+(a_2+b_2)c_2 \\ &=& a_1c_1+b_1c_1+a_2c_2+b_2c_2\\ &=& (a_1c_1+a_2c_2)+(b_1c_1+b_2c_2)\\ &=& \vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c}\\ \end{eqnarray}2,4,5も同様にして示すことができる

文字式の計算とほとんど同じだね!

だから,あまり違和感なく計算できるよ!
1 $\vec{a}\cdot\vec{a}=|\vec{a}|^2$ だけはベクトル特有だから注意!
大きさの2乗と内積の計算

$|〇|^2$ や内積の計算について考えてみよう!
以上より
$|\vec{a}+\vec{b}|^2=|\vec{a}|^2+2\vec{a}\cdot\vec{b}+|\vec{b}|^2$
が成り立つ
これは
$(a+b)^2=a^2+2ab+b^2$
の式と似通っている
他の例も考えてみよう
これは
$(2a-b)^2=4a^2-4ab+b^2$
と似通っている
これは
$(a+b)(a-b)=a^2-b^2$
と似通っている
以上より
$(a+2b)^2=a^2+4ab+4b^2$ だから
$|\vec{a}+2\vec{b}|^2=|\vec{a}|^2+4\vec{a}\cdot\vec{b}+4|\vec{b}|^2$
$(2a+b)(2a-b)=4a^2-b^2$ だから
$(2\vec{a}+\vec{b})(2\vec{a}-\vec{b}) =4|\vec{a}|^2-|\vec{b}|^2$
など
展開の式を参考にして計算を省略できる
内積の利用

内積を利用して問題を解いてみよう!
$|2\vec{a}-\vec{b}|≧0$ より
$|2\vec{a}-\vec{b}|=\sqrt{21}$

ベクトルの大きさに関する問題は,2乗して考えることが多い!
平行四辺形 $ABCD$ において,次のことが成り立つことを証明せよ。
$AC=DB$ ならば $AB \perp AD$
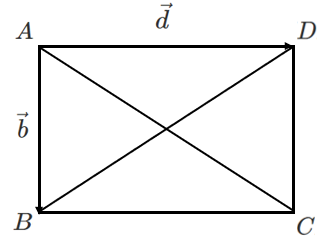
$\overrightarrow{AB}=\vec{b}$,$\overrightarrow{AD}=\vec{d}$ とすると
$\overrightarrow{AC}=\vec{b}+\vec{d}$,$\overrightarrow{DB}=\vec{b}-\vec{d}$
$AC=DB$ ならば,$|\overrightarrow{AC}|=|\overrightarrow{DB}|$ であるから
$|\vec{b}+\vec{d}|=|\vec{b}-\vec{d}|$
両辺2乗して
$|\vec{b}+\vec{d}|^2=|\vec{b}-\vec{d}|^2$
$|\vec{b}|^2+2\vec{b}\cdot\vec{d}+|\vec{d}|^2=|\vec{b}|^2-2\vec{b}\cdot\vec{d}+|\vec{d}|^2$
よって
$\vec{b}\cdot\vec{d}=0$
したがって,$\overrightarrow{AB}\perp\overrightarrow{AD}$ となるので(垂直条件)
$AB \perp AD$

$AB \perp AD$ を示すために,$\overrightarrow{AB}=\vec{b}$,$\overrightarrow{AD}=\vec{d}$ として,$\vec{b}\cdot\vec{d}$ を示す!
まとめ
● 内積の性質
1 $\vec{a}\cdot\vec{a}=|\vec{a}|^2$
2 $\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}$
3 $(\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c}$
4 $\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}$
5 $(k\vec{a})\cdot\vec{b}=\vec{a}\cdot k\vec{b}=k(\vec{a}\cdot\vec{b})$ $k$ は定数

内積を用いた計算は超重要!




コメント