高校数学Ⅱで学ぶ『円と直線の位置関係と $d$、$r$ の大小』について解説!
$d$ は円の中心と直線の距離、$r$ は円の半径のこと!
$d$ と $r$ の大小関係によって、円と直線の位置関係は決まる!
この投稿を見れば、『円と直線の位置関係と $d$、$r$ の大小』についてバッチリ!
円と直線の位置関係

円と直線の位置関係は3パターン!

円と直線の位置関係と判別式
円と直線の位置関係は以下のようになる
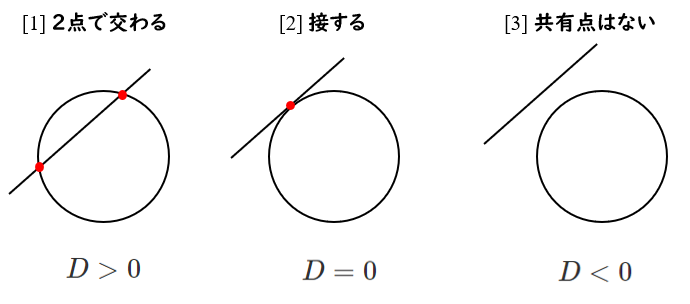
詳しくはこれ↓

円の中心と直線の距離 $d$ と円の半径 $r$ の大小

「円の中心と直線の距離 $d$ 」と「円の半径 $r$ 」の大小関係を調べれば,円と直線の位置関係を調べることができる!
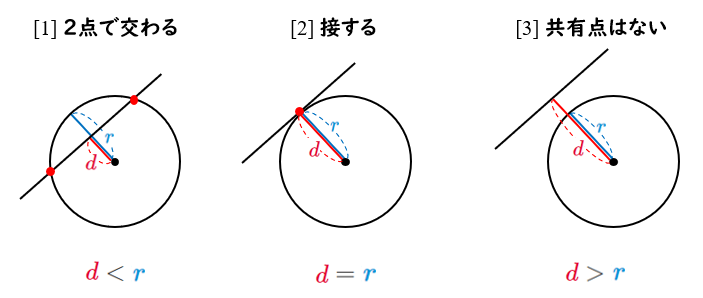

忘れても図を描けば思い出せるように!
問題
円の中心 $(0,0)$ と直線 $3x-4y+5=0$ の距離 $d$ は
$\displaystyle{d=\frac{|3\cdot0-4\cdot0+5|}{\sqrt{3^2+(-4)^2}}=1}$ 点と直線の距離
円と直線が接するとき,$d=r$ が成り立つので $r=1$
円の中心 $(0,0)$ と直線 $3x-4y+5=0$ の距離 $d$ は
$\displaystyle{d=\frac{|3\cdot0-4\cdot0+5|}{\sqrt{3^2+(-4)^2}}=1}$
円と直線が2点で交わるとき,$d<r$ が成り立つので $r>1$
円の中心 $(0,0)$ と直線 $3x-4y+5=0$ の距離 $d$ は
$\displaystyle{d=\frac{|3\cdot0-4\cdot0+5|}{\sqrt{3^2+(-4)^2}}=1}$
円と直線が交わらないとき,$d>r$ が成り立つので $0<r<1$
判別式と $d$,$r$ の大小の使い分け

「判別式」と「$d$,$r$ の大小」の使い分けはどうやってすればいいのかな?

上の問題を判別式 $D$ で解いてみよう!
$3x-4y+5=0$ より $\displaystyle{y=\frac{3}{4}x+\frac{5}{4}}$
$x^2+y^2=r^2$ に代入すると
$\displaystyle{x^2+(\frac{3}{4}x+\frac{5}{4})^2=r^2}$
$\displaystyle{x^2+\frac{9}{16}x^2+\frac{15}{8}x+\frac{25}{16}=r^2}$
$\displaystyle{\frac{25}{16}x^2+\frac{15}{8}x+\frac{25}{16}-r^2=0}$
$25x^2+30x-16r^2+25=0$
この2次方程式の判別式を $D$ とすると
$\displaystyle{\frac{D}{4}=15^2-25\cdot(-16r^2+25)}$
$=400r^2-400$
円と直線が接するので,$D=0$ より
$400r^2-400=0$
$r^2=1$
$r=±1$
$r>0$ より $r=1$

判別式で解く方が計算量が多いね!
直線の方程式に分数が含まれる場合は,「$d$,$r$ の大小」を用いた方が楽に解けそう!

計算してみて大変そうなら,方針を変えて解くようにしよう!
まとめ
● 円と直線の位置関係と $d$,$r$ の大小


$d$ と $r$ の大小を用いて位置関係を調べられるようになろう!




コメント