円と直線の位置関係

円と直線の位置関係は3パターン!
[1] 2点で交わる
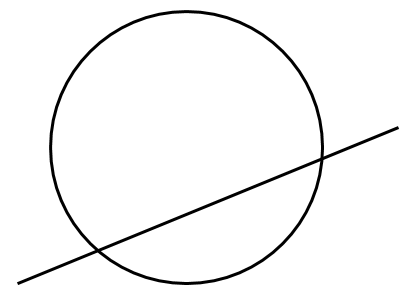
[2] 接する(1点で交わる)

[3] 交わらない
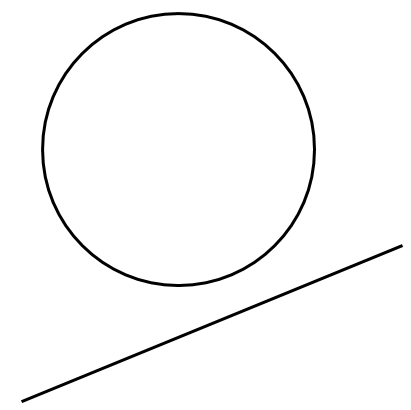
円と直線が接する

円と直線が1点で交わるとき,「円と直線は接する」という!
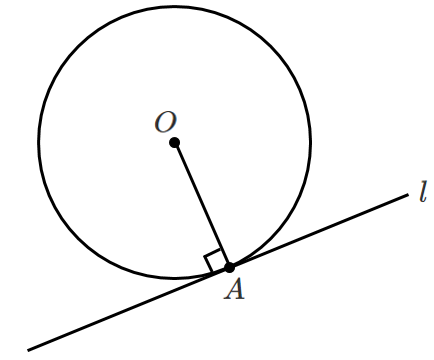
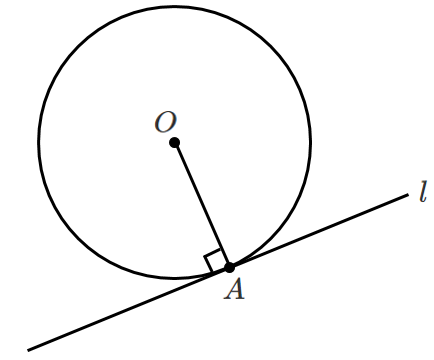
直線 $l$ を円 $O$ の接線
点 $A$ を接点 という

直線を水平にすると,垂直であることが直感的に分かるよ!
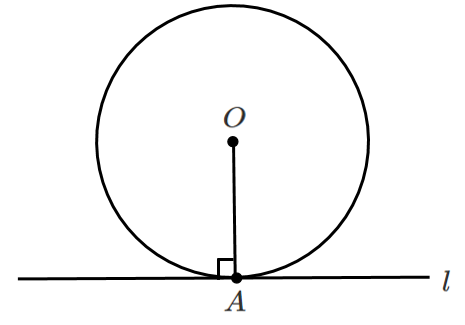

地面にボールが落ちていると考えたら,たしかに垂直だね!

直線が斜めでも,中心と接点を結んだら接線と垂直に交わることに気付けるようにしよう!
接線の長さ
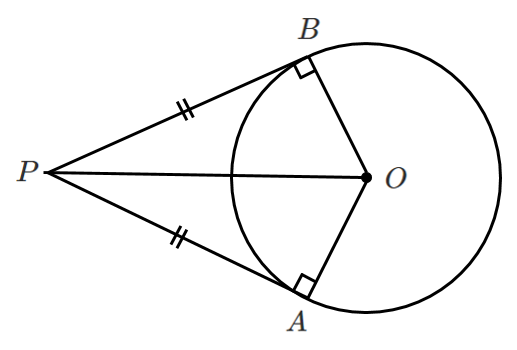
円 $O$ には外部の点 $P$ から2本の接線が引ける
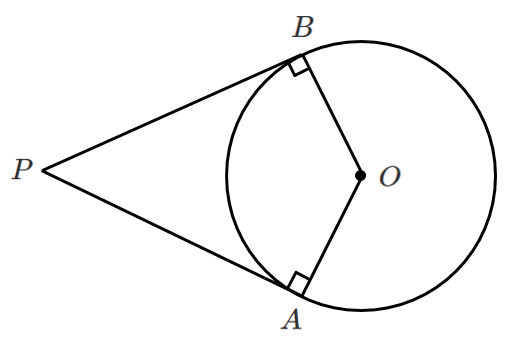
接点を $A$,$B$ とするとき,
線分 $PA$,$PB$ を 接線の長さ という
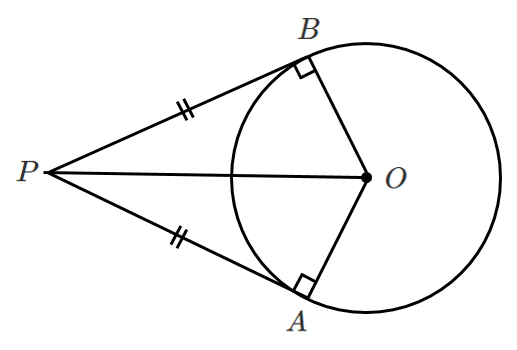

$OP$ が共通
$OA=OB$ より
$\triangle OAP\equiv\triangle OBP$
だから,$PA=PB$ が成り立つよ!
接線の長さの性質を利用する問題
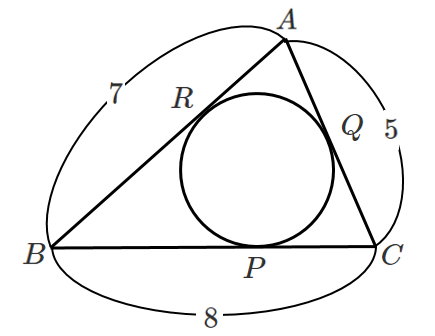
$BP=x$ とすると
$BR=x$
$AR=AQ=7-x$
$CP=CQ=8-x$
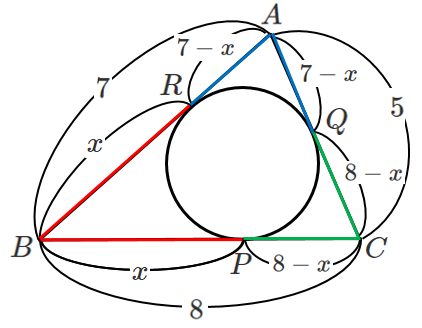
辺 $AC$ において
$(7-x)+(8-x)=5$
$x=5$
よって $BP=5$

三角形の内接円に関する問題は,接線の長さの性質が使えるね!
まとめ
● 直線と円が接する
$OA\perp l$
● 接線の長さの性質
円の外部の点から引いた2本の接線の長さは等しい
$PA=PB$
問題
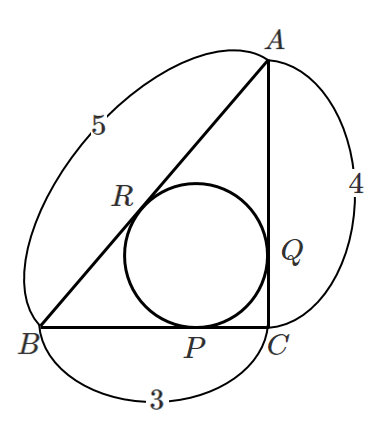
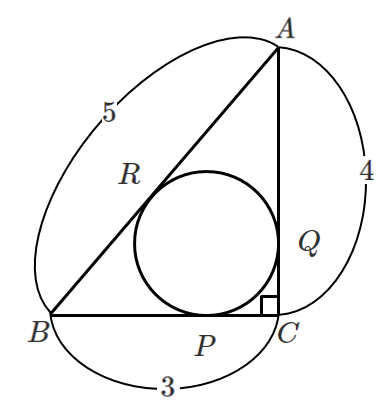
(1) $BP$ の長さを求めよ。
$BP=x$ とすると
$BR=x$
$AR=AQ=5-x$
$CP=CQ=3-x$
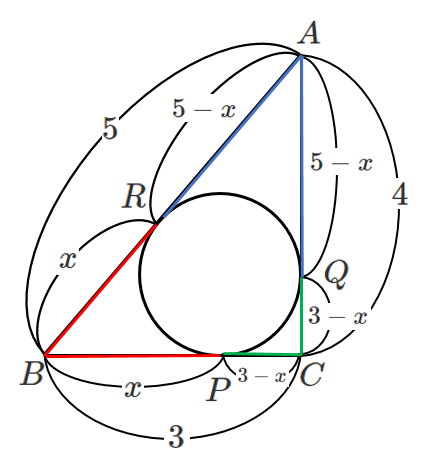
辺 $AC$ において
$(5-x)+(3-x)=4$
$x=2$
よって $BP=2$
(2) 内接円の半径を求めよ。
$AB^2=AC^2+BC^2$ が成り立つので
$\triangle ABC$ は $\angle C=90^\circ$ の直角三角形
内接円の中心を $I$ とすると
$IP\perp BC$,$IQ\perp AC$
$IP=IQ$ より
四角形 $IPCQ$ は正方形である
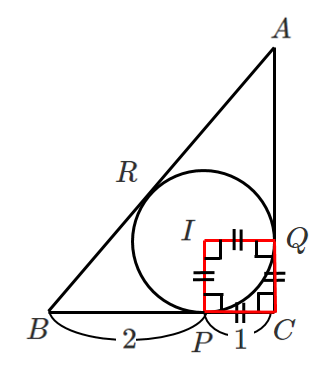
(1) より $CP=1$ なので
内接円の半径は $1$

接線の長さが等しいことを知っていれば,簡単に解ける!




コメント