円順列とは
円順列 … ものを円形に並べる順列

普通の順列と何が違うのかな?

まずは円順列のルールを知ろう!
円順列のルール
円順列のポイント
回転して並びが同じになるものは同じ並び方とみなす

具体例を使って考えてみよう!
円を4等分した各部分を4色で塗り分けるとき,塗り方は何通りか
例えば,下の4つは
赤に着目すると,
時計回りに 青→緑→黄 になっている
回転すると同じ並びになるので,
下の4つは円順列として同じ並びとみなす
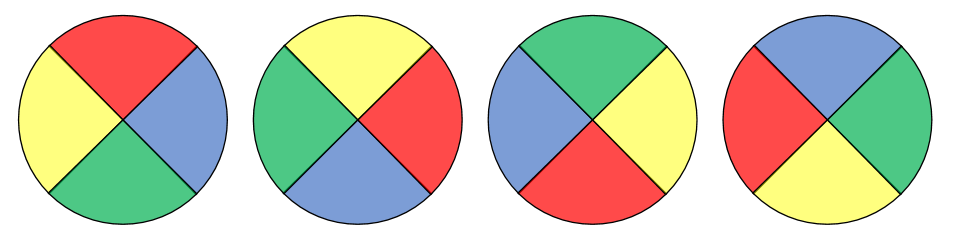
円順列の考え方
順列の復習はこれ↓

順列
順列の基本!「nPr」と「n!」の使い方をマスターしよう!

円順列ってどうやって考えたらいいのかな?

回転したら同じ並びができてしまうから,
回転しないように1つを固定して考えるよ!
円順列のポイント
1つを固定したら順列で考えることができる
赤を固定すると
$A,B,C$ を3色で塗り分ければよい
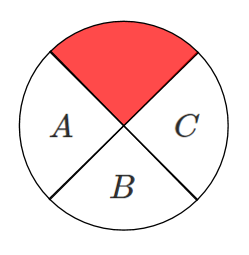
3色を $A,B,C$ に並べるので
$3!=3・2・1=6$ (通り)
全ての塗り方を下に示す
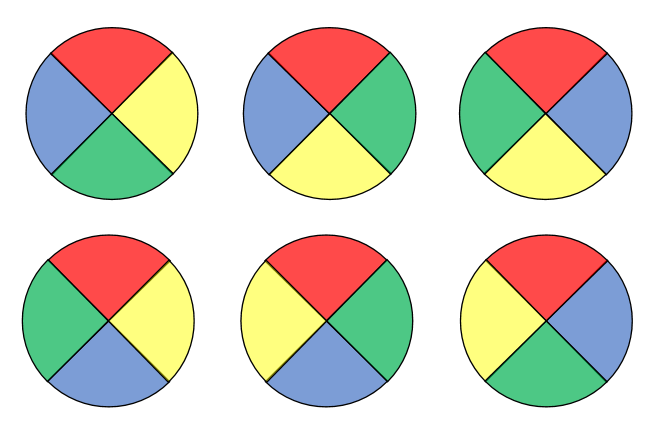

一つを固定しておけば,回転して同じ並びになることはないね!
円順列の総数
円順列の総数
異なる $n$ 個の円順列の総数は $(n-1)!$
異なる $n$ 個のうち
1つを固定して考えるので
その1つを除いた $(n-1)$ 個の順列が
円順列の総数である
円を5等分した各部分を5色で塗り分けるとき,塗り方は何通りか
1色を固定すると
残り4色の順列になるので
$(5-1)!=4!=4・3・2・1=24$ (通り)

$(n-1)!$ の $-1$ は固定した1つを除いたということ!
理屈を理解してから解くことが大切だね!
まとめ
● 円順列のルール
回転して並びが同じになるものは同じ並び方とみなす
● 円順列の考え方
回転しないように1つを固定して順列として考える
● 円順列の総数
異なる $n$ 個の円順列の総数は $(n-1)!$
$n$ 個のうち1つを固定した残りの $(n-1)$ 個の順列
問題
次のものの総数を求めよ。
(1) 6人が輪の形に並ぶときの並び方
(2) 色の異なる7個の玉を円形に並べる置き方
(1) 6人が輪の形に並ぶときの並び方
(2) 色の異なる7個の玉を円形に並べる置き方
(1) 6人が輪の形に並ぶときの並び方
$(6-1)!=5!=5・4・3・2・1=120$ (通り)
(2) 色の異なる7個の玉を円形に並べる置き方
$(7-1)!=6!=6・5・4・3・2・1=720$ (通り)

$(n-1)!$ の $-1$ の意味をきちんとおさえれば完璧!




コメント