
9個を並べるから $9!$ になるのかな?

$9!$ では間違いになるよ!
順列から復習しよう!
順列

$n!$ がどういうときに使えるか確認しよう!
$n!$ … 異なる $n$ 個すべてを並べる順列の総数
異なる9個すべてを並べる順列なので $9!$
同じものが含まれているので $9!$ はダメ

なんで同じものを含むと $9!$ ではダメなんだろう?



同じものが含まれるか含まれないかで順列の総数が変わるよ!
順列の復習はこれ↓

同じ文字を含む順列の考え方

同じ文字を含む順列は組合せ $_nc_r$ を用いたら解けるよ!
$_nC_r$ を使った解き方
①9個の場所を用意する

②9個の場所から $a$ を置く場所を4個を選ぶ
→同じものの並び方は1通りなので選ぶだけでよい

9個から4個選ぶので $_9C_4$ 通り
③残り5個の場所から $b$ を置く場所を3個選ぶ
→同じものの並び方は1通りなので選ぶだけでよい

5個から3個選ぶので $_5C_3$ 通り
④残り2個の場所から $c$ を置く場所を2個選ぶ
→同じものの並び方は1通りなので選ぶだけでよい
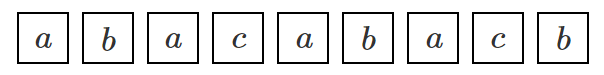
2個から2個選ぶので $_2C_2$ 通り
積の法則より $_9C_4 × _5C_3 × _2C_2$

順列なのに組合せの $_nC_r$ を使うことが意外だね!
$!$ を使った解き方

$_9C_4 × _5C_3 × _2C_2$ を式変形すると,
順列の「$!$」 を使った式で表すこともできるよ!
$_9C_4 × _5C_3 × _2C_2$
$\displaystyle{=\frac{9・8・7・6}{4・3・2・1}×\frac{5・4・3}{3・2・1}×\frac{2・1}{2・1}}$
$\displaystyle{=\frac{9・8・7・6・5・4・3・2・1}{(4・3・2・1)(3・2・1)(2・1)}}$
$\displaystyle{=\frac{9!}{4!3!2!}}$
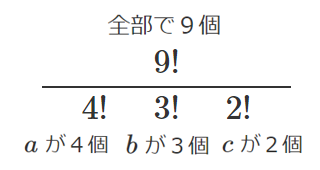

「$!$」を使っても計算できるね!
同じものを含む順列の総数
あるとき,それらを1列で並べる順列の総数は
$\displaystyle{\frac{n!}{p!q!r!}}$ ($n=p+q+r$)
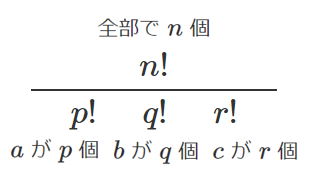
まとめ
● 同じものを含む順列
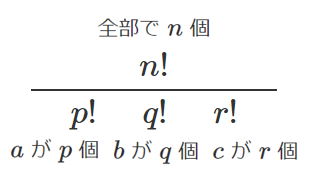
$_nC_r$ を使って解くこともできる
問題
(1) $1$ を3個,$2$ を2個,$3$ を2個すべてを並べる
(2) 6文字 $BANANA$ をすべて使った文字列
(1) $1$ を3個,$2$ を2個,$3$ を2個すべてを並べる
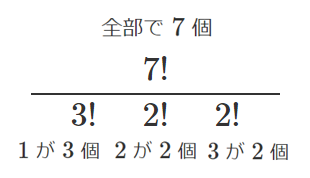
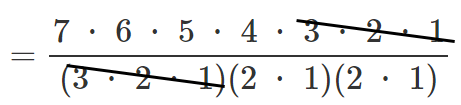
$=210$ (通り)
(2) 6文字 $BANANA$ をすべて使った文字列
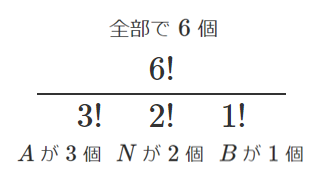
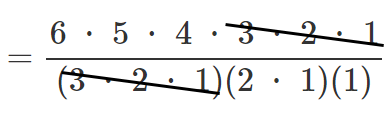
$=60$ (通り)

順列に同じものが含まれている場合は,しっかり解けるようにしよう!




コメント