2文字以上を含む式の因数分解には「最低次数の文字について整理する」ことが重要です!
次数が同じ場合は,どちらかの文字に着目して整理した後,たすき掛けをして因数分解する必要があります!
因数分解の中では難易度が高めですが,わかりやすく解説します!

今回の問題はこれ!
(1) $x^2+5xy+5x+6y^2+11y+4$
(2) $2x^2-5xy-3y^2+x+11y-6$
次数とは
次数とは,かけ合わせた文字の個数のこと。
例(単項式の場合)
$2x^3$ は $x$ が $3$ 個かけ合わされているので,次数は $3$
例(多項式の場合)
$2x^3+x^2$ は,$2x^3$ の次数が $3$, $x^2$ の次数が $2$ なので,大きい値である $3$ が次数
例(特定の文字に着目した場合)
$2x^4y^2+3xy^3$ は,$x$ に着目すると次数は $4$,$y$ に着目すると次数は $3$
2文字以上が含まれる場合の因数分解の手順
・因数分解の公式が使えない(因数分解の公式を使う方法)
・式全体を共通因数でくくれない(共通因数でくくる因数分解の方法)
・置き換えが使えない(置き換えを用いて因数分解する方法)
このような2文字以上が含まれる式の因数分解では,まず初めに次数の比較をする必要があります
次数が同じ場合は,どちらかの文字で整理して「たすき掛け」を用いる
$x^2+5xy+5x+6y^2+11y+4$ は,
$x$ に着目すると次数が $2$,$y$ に着目すると次数が $2$
次数が同じなので,どちらかの文字について整理して「たすき掛け」を用いることがポイントになります
次数が異なる場合の因数分解はこれ↓

「たすき掛け」の基本はこれ↓

問題
(1) $x^2+5xy+5x+6y^2+11y+4$
(2) $2x^2-5xy-3y^2+x+11y-6$
(1) $x^2+5xy+5x+6y^2+11y+4$
$x$ も $y$ も次数が同じなので,
$x$ について整理すると($y$ ついて整理してもよい)
$x^2+5xy+5x+6y^2+11y+4$
$=x^2+(5y+5)x+(6y^2+11y+4)$ ← $x$ について降べきの順に整理
$=x^2+(5y+5)x+(2y+1)(3y+4)$ ← 後ろのかっこを因数分解
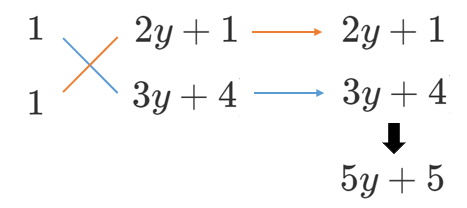
$=\{x+(2y+1)\}\{x+(3y+4)\}$ ← たすき掛け
$=(x+2y+1)(x+3y+4)$
(2) $2x^2-5xy-3y^2+x+11y-6$
$x$ も $y$ も次数が同じなので,
$x$ について整理すると($y$ ついて整理してもよい)
$2x^2-5xy-3y^2+x+11y-6$
$=2x^2+(-5y+1)x-(3y^2-11y+6)$ ← $x$ について降べきの順に整理
$=2x^2+(-5y+1)x-(y-3)(3y-2)$ ← 後ろのかっこを因数分解
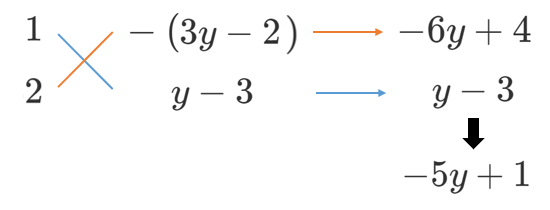
$=\{x-(3y-2)\}\{2x+(y-3)\}$ ← たすき掛け
$=(x-3y+2)(2x+y-3)$
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント