高校数学Ⅱで学ぶ『因数定理』についてわかりやすく解説!
『因数定理』は3次以上の整式を因数分解するときに使う公式です!
「因数を見つけるコツ」や「組み立て除法」も解説しています!
因数とは
例えば、$x^2-5x-6=(x+1)(x-6)$ と式変形できる
このとき、$x+1$ と $x-6$ は $x^2-5x-6$ の因数である
$x^2-5x-6=(x+1)(x-6)$ と式変形することを因数分解といい、
因数分解は文字通り「因数に分解すること」である
因数定理
『因数定理』とは、整式の因数を見つけるときに使う定理のことです。
【証明】
$P(x)$ が $x-k$ を因数にもつとき,次のように表せる
$P(x)=(x-k)Q(x)$
$x=k$ を代入すると, $P(k)=0$
よって,$P(x)$ が $x-k$ を因数にもつとき $P(k)=0$
因数定理の利用
$P(x)=x^3-x^2-x-2$ とすると,
$P(1)$$=1^3-1^2-1-2=$$-3$
$P(x)$ は $x-1$ を因数にもたない
$P(-1)$$=(-1)^3-(-1)^2-(-1)-2=$$-3$
$P(x)$ は $x+1$ を因数にもたない
$P(2)$$=2^3-2^2-2-2=$$0$
$P(x)$ は $x-2$ を因数にもつ
因数を見つけ方
因数定理を利用して、整式 $P(x)$ の因数を見つける際に、
$x=1$ → $x=-1$ → $x=2$ → $x=-2$ → $x=3$ → …
と順番に代入すれば、因数が見つかりそうだが、より効率的に確実に因数を見つける方法がある。
最高次の項の係数が $1$ なら $\boldsymbol{±(定数項の約数)}$ を調べる
最高次の項の係数が $1$ 以外なら $\displaystyle{\boldsymbol{\pm\frac{(定数項の約数)}{(最高次の項の係数の約数)}}}$ を調べる
$P(x)=2x^3+x^2+5x-3$ とする
最高次の項は $2$ なので、$\displaystyle{\boldsymbol{\pm\frac{(定数項の約数)}{(最高次の項の係数の約数)}}}$ を調べる
すなわち $\displaystyle{\pm\frac{(3の約数)}{(2の約数)}}$ なので,$\displaystyle{x=\pm1,\pm3,\pm\frac{1}{2},\pm\frac{3}{2}}$ を調べる
$P(1)=2\cdot1^3+1^2+5\cdot1-3=5$
$P(-1)=2\cdot(-1)^3+(-1)^2+5\cdot(-1)-3=-9$
$P(3)=2\cdot3^3+3^2+5\cdot3-3=75$
$P(-3)=2\cdot(-3)^3+(-3)^2+5\cdot(-3)-3=-63$
$\displaystyle{P\left(\frac{1}{2}\right)=2\cdot\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^2+5\cdot\frac{1}{2}-3=0}$
$\displaystyle{P\left(\frac{1}{2}\right)=0}$ より、$P(x)$ は $\displaystyle{x-\frac{1}{2}}$ を因数にもつ
3次式の因数分解
『因数定理』は3次以上の整式を因数分解するときに使います。
② 因数分解したい式を因数で割る
③ ($1$ 次式)($2$ 次式) となるので $2$ 次式が因数分解できたら因数分解する
① 因数定理を用いて因数を見つける
$P(x)=x^3-6x^2+11x-6$ とすると
$P(1)=1^3-6\cdot1^2+11\cdot1-6=0$
$P(1)=0$ より,$P(x)$ は $x-1$ を因数にもつ
② 因数分解したい式を因数で割る
$P(x)$ を $x-1$ で割る
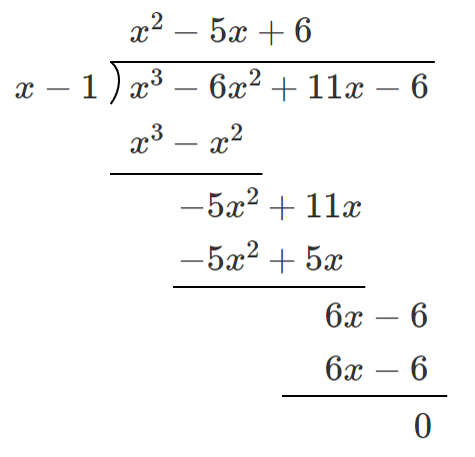
以上より, $x^3-6x^2+11x-6=(x-1)(x^2-5x+6)$
③ ($1$ 次式)($2$ 次式) となるので $2$ 次式が因数分解できたら因数分解する
$x^3-6x^2+11x-6$
$=(x-1)(x^2-5x+6)$
$=(x-1)(x-2)(x-3)$
4次式の因数分解
② 因数分解したい式を因数で割る
③ ($1$ 次式)($3$ 次式) となるので $3$ 次式を因数分解する

3次以上の整式でも「因数定理」を用いれば,因数分解できるね!
組み立て除法

筆算よりも簡単な割り算の計算方法「組み立て除法」を学ぼう!
割られる式 $x^3-6x^2+11x-6$ の係数を並べる
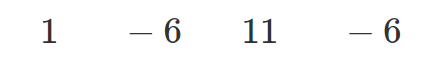
割る式 $x-2$ に代入して $0$ になる数 $2$ を右に書く

左の数を下ろす
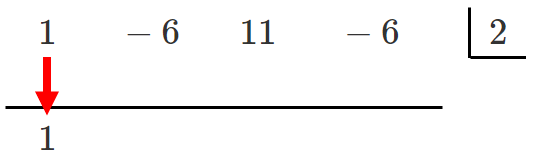
右上の数をかける
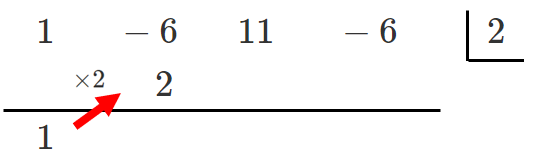
上下を足す
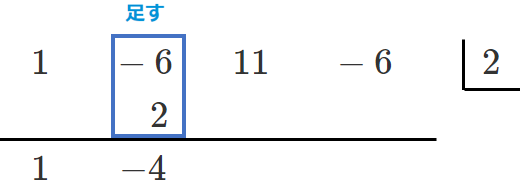
これを繰り返す
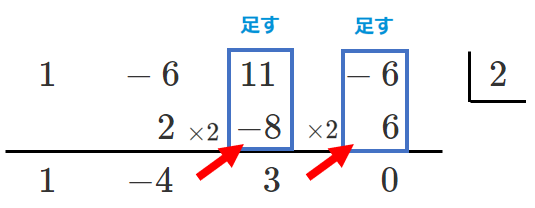
下に出てきた数が商の係数と余り
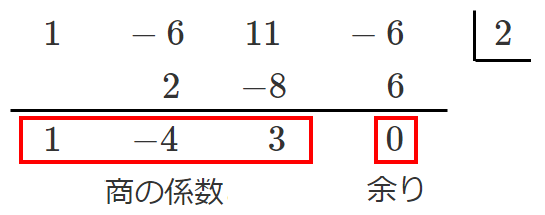
商は $x^2-4x+3$ 余りは $0$

筆算するよりも早く計算できるね!

「因数定理」で因数が見つかったら「組み立て除法」をしよう!
問題
(1) $x^3-4x^2+x+6$
(2) $x^3-x^2-8x+12$
(3) $2x^4-3x^3+7x^2+7x-5$
(1) $x^3-4x^2+x+6$ ← $\pm(6の約数)$ を調べる
(2) $x^3-x^2-8x+12$ ← $\pm(12の約数)$ を調べる
(3) $2x^4-3x^3+7x^2+7x-5$ ← $\displaystyle{\pm\frac{(5の約数)}{(2の約数)}}$ を調べる
(1) $x^3-4x^2+x+6$
$P(x)=x^3-4x^2+x+6$ とすると
$P(-1)=(-1)^3-4\cdot(-1)^2+(-1)+6=0$
$P(x)$ は $x+1$ を因数にもつ
$P(x)=(x+1)(x^2-5x+6)$
$=(x+1)(x-2)(x-3)$
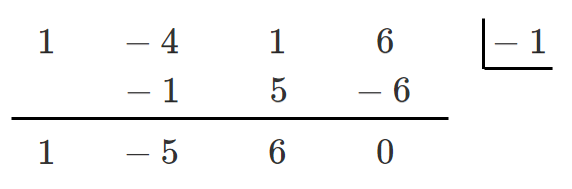
(2) $x^3-x^2-8x+12$
$P(x)=x^3-x^2-8x+12$ とすると
$P(2)=2^3-2^2-8\cdot2+12=0$
$P(x)$ は $x-2$ を因数にもつ
$P(x)=(x-2)(x^2+x-6)$
$=(x-2)(x-2)(x+3)$
$=(x-2)^2(x+3)$
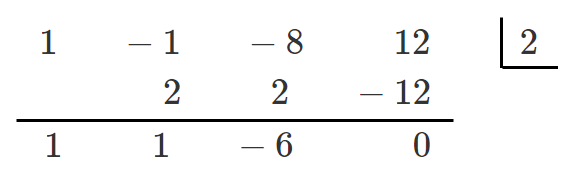
(3) $2x^4-3x^3+7x^2+7x-5$
$P(x)=2x^4-3x^3+7x^2+7x-5$ とすると
$P(-1)=0$ より,$P(x)$ は $x+1$ を因数にもつ
$P(x)=(x+1)(2x^3-5x^2+12x-5)$
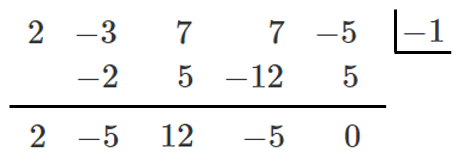
$Q(x)=2x^3-5x^2+12x-5$ とすると
$\displaystyle{Q\left(\frac{1}{2}\right)=0}$ より,$Q(x)$ は $\displaystyle{x-\frac{1}{2}}$ を因数にもつ
$\displaystyle{Q(x)=\left(x-\frac{1}{2}\right)(2x^2-4x+10)}$
$=(2x-1)(x^2-2x+5)$
したがって $P(x)=(x+1)(2x-1)(x^2-2x+5)$
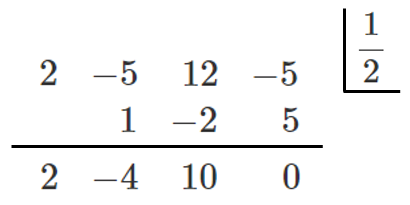
まとめ
● 因数とは
積の形で表したときの,かけ合わされているひとつひとつ
● 因数定理
$P(x)$ が $x-k$ を因数にもつとき $P(k)=0$
代入して $0$ になる数を探す
● 3次式の因数分解
① 因数定理を用いて因数を見つける
② 因数分解したい式を因数で割る
③ ($1$ 次式)($2$ 次式) となるので $2$ 次式が因数分解できたら因数分解する
● 組み立て除法
筆算よりも簡単な割り算の計算方法

計算は数学の基本!
3次式の因数分解をきちんとマスターしよう!




コメント