数学Ⅱで学ぶ『多項定理の一般項』を利用した問題をわかりやすく解説します!
重要なのは多項定理の一般項の基本をおさえながら問題演習を積むことです!
多項定理が苦手な人はぜひ参考にしてください!

この投稿で扱う問題はこれ!
$(x^2+2x-1)^6$ の展開式における一般項は
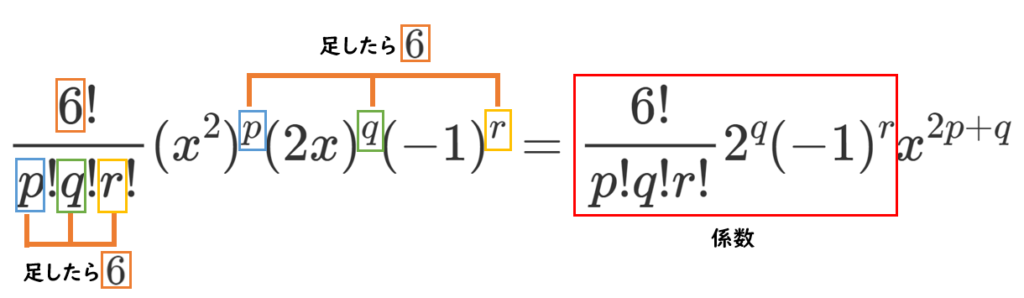
ただし、$p$,$q$,$r$ は $0$ 以上の整数で $p+q+r=6$
$x^7$ の係数を求めるので $2p+q=7$ここをタッチ!
未知数3つに対し、方程式が2つであるから、係数が大きい文字 $p$ の範囲を考える。
そのために、$q=7-2p$ と式変形して $0≦q≦6$ から $p$ の範囲を求める。
すなわち $q=7-2p$
$0≦q≦6$ であるから $0≦7-2p≦6$
これを解いて $\displaystyle{\frac{1}{2}≦p≦\frac{7}{2}}$
$p$ は $0$ 以上の整数なので $p=1,2,3$ ← $p$ が絞り込めた!
$p=1$ のとき $q=5,r=0$
$p=2$ のとき $q=3,r=1$
$p=3$ のとき $q=1,r=2$
ここをタッチ!
※ $0!=1$,$(-1)^0=1$
多項定理とは
「$(a+b+c)^5$ の展開式で $a^2b^2c$ の係数を求めよ」
展開するのはさすがに大変ですよね。
こういった問題を解くときに、『多項定理』を使います。
二項定理と同様に、一般項を考えることで係数を求めることができます。
二項定理が苦手な人は、まずはこれ↓↓

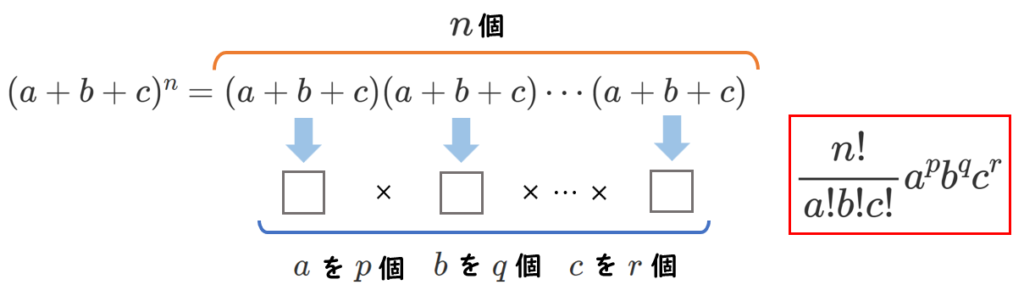
$(a+b+c)^n$ の展開式の一般項は
$\displaystyle{\frac{n!}{a!b!c!}a^pb^qc^r}$
($p+q+r=n$,$p≧0$,$q≧0$,$r≧0$)
$(a+b+c)^n$ の一般項は、『$n$ 個の ( ) の中から $a$ を $p$ 個、$b$ を $q$ 個、$c$ を $r$ 個取り出す』と考えて、
$\displaystyle{\frac{n!}{p!q!r!}a^pb^qc^r}$
($p+q+r=n$,$p≧0$,$q≧0$,$r≧0$)
と表すことができる。
詳しくはこの記事を参考にしてください↓↓

問題
<解答の手順>
1. 一般項をつくる ※指数法則に注意
2. 条件から $p$,$q$,$r$ を絞り込む
➡1つの文字に着目して不等式を作る
3. $p$,$q$,$r$ を代入して係数を求める
$(x^2+2x-1)^6$ の展開式における一般項は
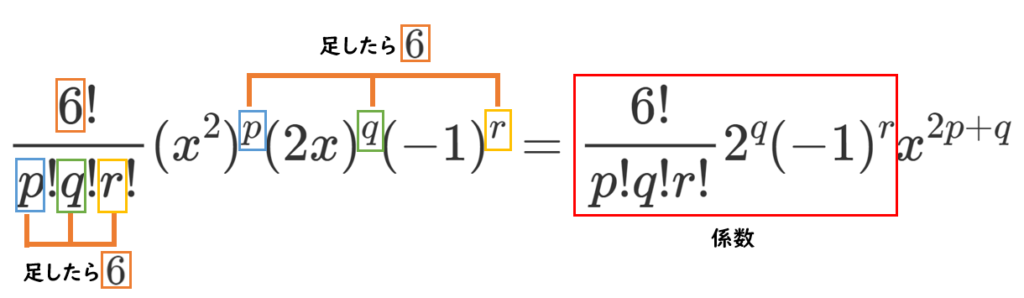
ただし、$p$,$q$,$r$ は $0$ 以上の整数で $p+q+r=6$
$x^7$ の係数を求めるので $2p+q=7$ここをタッチ!
未知数3つに対し、方程式が2つであるから、係数が大きい文字 $p$ の範囲を考える。
そのために、$q=7-2p$ と式変形して $0≦q≦6$ から $p$ の範囲を求める。
すなわち $q=7-2p$
$0≦q≦6$ であるから $0≦7-2p≦6$
これを解いて $\displaystyle{\frac{1}{2}≦p≦\frac{7}{2}}$
$p$ は $0$ 以上の整数なので $p=1,2,3$ ← $p$ が絞り込めた!
$p=1$ のとき $q=5,r=0$
$p=2$ のとき $q=3,r=1$
$p=3$ のとき $q=1,r=2$
ここをタッチ!
※ $0!=1$,$(-1)^0=1$




コメント