数学Ⅱで学ぶ『多項定理』を解説します!
『多項定理』は 「$(a+b+c)^5$ の展開式で $a^2b^2c$ の係数を求めよ」という問題に使われます!
『二項定理』と似ていますが、式の展開の仕組みを理解することで、多項定理の理解が深まり、問題を解くのが非常に楽になります!
この投稿では、多項定理の原理とその使い方を例を交えながら、わかりやすく解説します!
多項定理が苦手な人はぜひ参考にしてください!

この投稿で扱う問題はこれ!
(2) $(a-b-c)^6$ における $ab^3c^2$ の係数を求めよ。
(3) $(2x-3y+z)^5$ における $x^2yz^2$ の係数を求めよ。
(1) $(a+b+c)^5$ [$a^2b^2c$]
$(a+b+c)^5$ の一般項は $\displaystyle{\frac{5!}{p!q!r!}a^pb^qc^r}$ ($p+q+r=5$)
求める項は $p=2$,$q=2$,$r=1$ なので、その係数は $\displaystyle{\frac{5!}{2!2!1!}=30}$
【別解】『5個の ( ) の中から $a$ を2個、$b$ を2個、$c$ を1個取り出す』
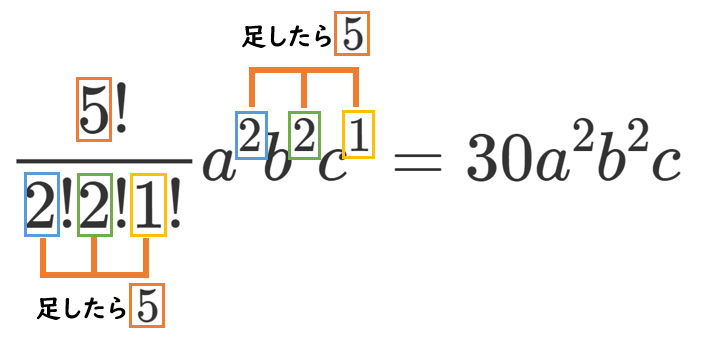
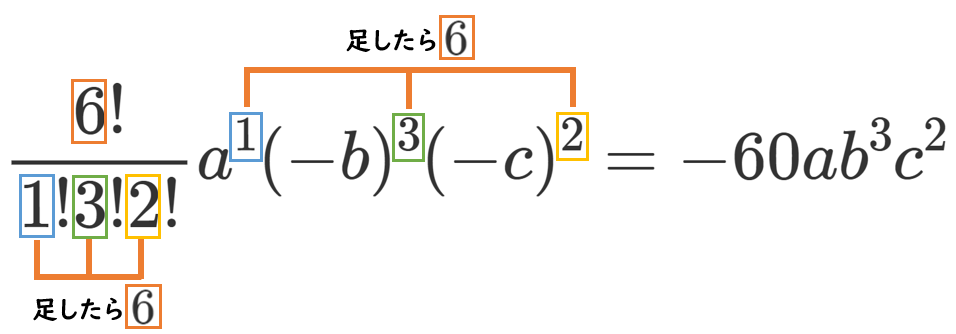
(2) $(a-b-c)^6$ [$ab^3c^2$]
$(a-b-c)^6$ の一般項は $\displaystyle{\frac{6!}{p!q!r!}a^p(-b)^q(-c)^r}$ ($p+q+r=6$)
求める項は $p=1$,$q=3$,$r=2$ なので、 $\displaystyle{\frac{6!}{1!3!2!}a^1(-b)^3(-c)^2=-60ab^3c^2}$
求める係数は $-60$
【別解】『6個の ( ) の中から $a$ を1個、$-b$ を3個、$-c$ を2個取り出す』
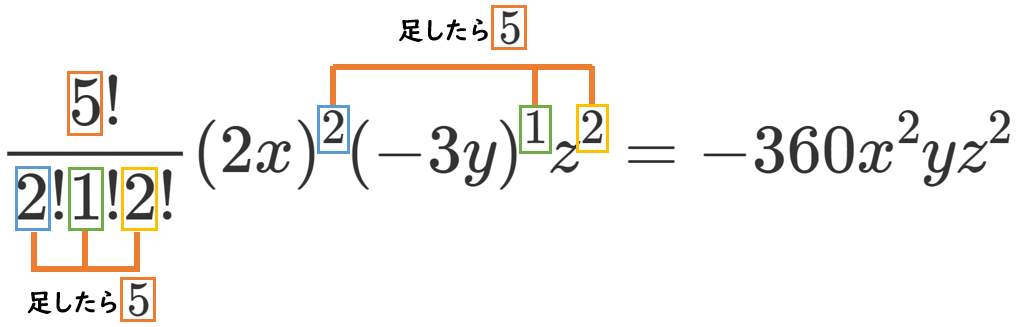
(3) $(2x-3y+z)^5$ [$x^2yz^2$]
$(2x-3y+z)^5$ の一般項は $\displaystyle{\frac{5!}{p!q!r!}(2x)^p(-3y)^qz^r}$ ($p+q+r=5$)
求める項は $p=2$,$q=1$,$r=2$ なので、 $\displaystyle{\frac{5!}{2!1!2!}(2x)^2(-3y)^1z^2=-360x^2yz^2}$
求める係数は $-360$
【別解】『5個の ( ) の中から $a$ を2個、$b$ を1個、$c$ を2個取り出す』
多項定理とは
「$(a+b+c)^5$ の展開式で $a^2b^2c$ の係数を求めよ」
展開するのはさすがに大変ですよね。
こういった問題を解くときに、『多項定理』を使います。
二項定理と同様に、一般項を考えることで係数を求めることができます。
二項定理が苦手な人は、まずはこれ↓↓

多項定理(3項の場合)
$(a+b+c)^n$ の展開式の一般項は
$\displaystyle{\frac{n!}{a!b!c!}a^pb^qc^r}$
($p+q+r=n$,$p≧0$,$q≧0$,$r≧0$)

二項定理はCだったのに、階乗(!)が出てきた!
おまけに文字も増えた気がする!
多項定理の説明(具体例)
$(a+b+c)^4$ を例に、『多項定理』を考えてみましょう。
『二項定理』でも説明しましたが、
式の展開は『それぞれの ( ) から1つずつ取り出してかける』という計算を行っています。
つまり、$(a+b+c)^4$ の展開は以下のようなイメージです。
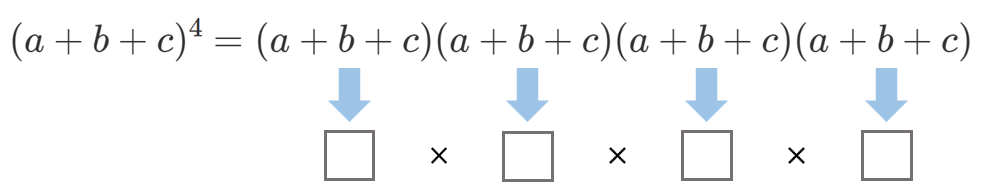
□には $a$、$b$、$c$ のいずれかが入ります。
すべて $a$ が取り出されると $a^4$ になります。
例えば、$a^2bc$ になるような取り出され方を考えると
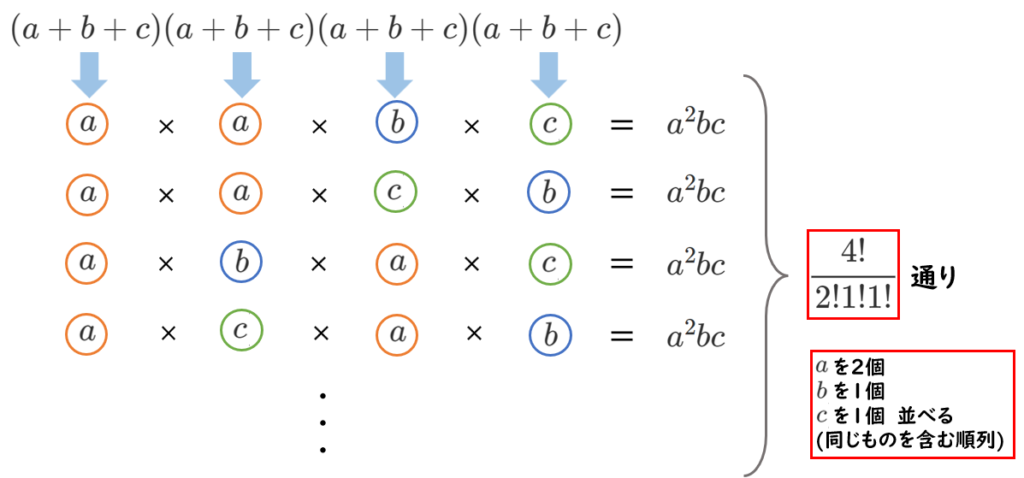
$a^2bc$ の取り出され方は、『$a$ を2個、$b$ を1個、$c$ を1個並べる順列(同じものを含む順)』の総数と同じであることがわかる。
つまり、$\displaystyle{\frac{4!}{2!1!1!}}$ 通りなので、$a^2bc$ の係数は $\displaystyle{\frac{4!}{2!1!1!}=12}$ である。

だから、多項定理の一般項に階乗(!)が出てくるのか!
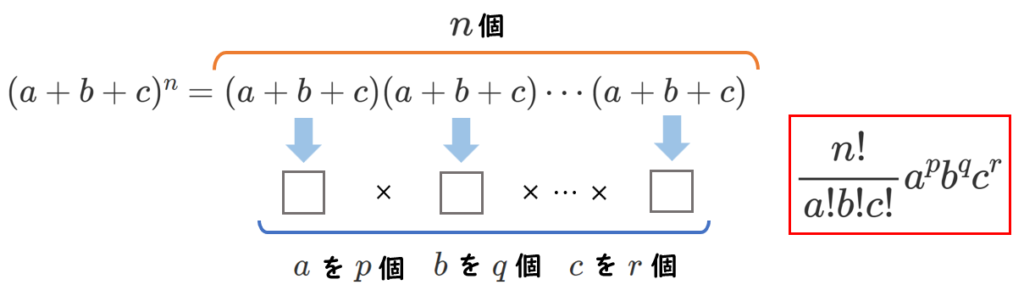
$(a+b+c)^n$ の一般項は、『$n$ 個の ( ) の中から $a$ を $p$ 個、$b$ を $q$ 個、$c$ を $r$ 個取り出す』と考えて、
$\displaystyle{\frac{n!}{p!q!r!}a^pb^qc^r}$
($p+q+r=n$,$p≧0$,$q≧0$,$r≧0$)
と表すことができる。
多項定理の証明(二項定理から)
二項定理を用いて、$(a+b+c)^n$ の展開式で $a^pb^qc^r$ ($p+q+r=n$) の項の係数を求めます。
$(a+b+c)^n=\{(a+b)+c\}^n$ と考えると、
二項定理より一般項は $_n C _{n-r}(a+b)^{n-r}c^r$
また、二項定理より $(a+b)^{n-r}$ の一般項は $_{n-r} C_q a^{n-r-q}b^q$
$n-r-q=p$ とおくと、$(a+b+c)^n$ の一般項は $_n C_{n-r} \times{_{n-r}C_q}a^pb^qc^r$
したがって、$a^pb^qc^r$ ($p+q+r=n$) の項の係数は
\begin{eqnarray} & & _n C_{n-r}\times{_{n-r}C_q} \\ & = & \frac{n!}{r!(n-r)!}\cdot\frac{(n-r)!}{(n-r-q)!q!} \\ & = & \frac{n!}{(n-r-q)!q!r!} \\ & = & \frac{n!}{p!q!r!} \end{eqnarray}問題
(2) $(a-b-c)^6$ における $ab^3c^2$ の係数を求めよ。
(3) $(2x-3y+z)^5$ における $x^2yz^2$ の係数を求めよ。
(1) $(a+b+c)^5$ [$a^2b^2c$]
$(a+b+c)^5$ の一般項は $\displaystyle{\frac{5!}{p!q!r!}a^pb^qc^r}$ ($p+q+r=5$)
求める項は $p=2$,$q=2$,$r=1$ なので、その係数は $\displaystyle{\frac{5!}{2!2!1!}=30}$
【別解】『5個の ( ) の中から $a$ を2個、$b$ を2個、$c$ を1個取り出す』
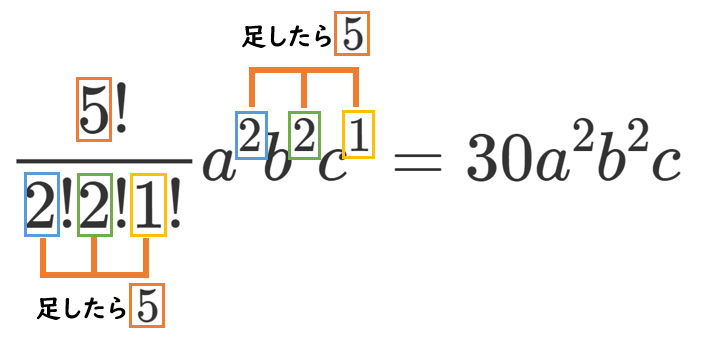
(2) $(a-b-c)^6$ [$ab^3c^2$]
$(a-b-c)^6$ の一般項は $\displaystyle{\frac{6!}{p!q!r!}a^p(-b)^q(-c)^r}$ ($p+q+r=6$)
求める項は $p=1$,$q=3$,$r=2$ なので、 $\displaystyle{\frac{6!}{1!3!2!}a^1(-b)^3(-c)^2=-60ab^3c^2}$
求める係数は $-60$
【別解】『6個の ( ) の中から $a$ を1個、$-b$ を3個、$-c$ を2個取り出す』

(3) $(2x-3y+z)^5$ [$x^2yz^2$]
$(2x-3y+z)^5$ の一般項は $\displaystyle{\frac{5!}{p!q!r!}(2x)^p(-3y)^qz^r}$ ($p+q+r=5$)
求める項は $p=2$,$q=1$,$r=2$ なので、 $\displaystyle{\frac{5!}{2!1!2!}(2x)^2(-3y)^1z^2=-360x^2yz^2}$
求める係数は $-360$
【別解】『5個の ( ) の中から $a$ を2個、$b$ を1個、$c$ を2個取り出す』

【補足】
多項定理は項がいくつあっても成り立ちます。
$(x_1+x_2+\cdots+x_m)^n$ の展開式における $x_1^{k_1}x_2^{k_2}\cdots x_m^{k_m}$ の係数は
$\displaystyle{\frac{n!}{k_1!k_2!\cdots k_m!}}$
($k_1+k_2+\cdots+k_m=n$,$k_1,k_2,\cdots,k_m≧0$)




コメント