
定積分で面積を求める方法を学ぼう!
定積分
$F'(x)=f(x)$ のとき
$\displaystyle{\int_a^b f(x) dx=\left[F(x)\right]_a^b=F(b)-F(a)}$
定積分の $\displaystyle{\int_a^b f(x) dx}$ において
$a$ を 下端(かたん),$b$ を 上端(じょうたん) という
定積分の $\displaystyle{\int_a^b f(x) dx}$ を求めることを
関数 $f(x)$ を $a$ から $b$ まで 積分する という
定積分の計算についてはこれ↓

定積分と面積

定積分を用いれば,曲線で囲まれる面積を求めることができる!
$a≦x≦b$ において,$f(x)≧0$ のとき(関数 $y=f(x)$ が $x$ 軸より上側のとき)
関数 $y=f(x)$,2直線 $x=a$,$x=b$,$x$ 軸で囲まれる部分の面積 $S$ は
$\displaystyle{S=\int_a^b f(x) dx}$
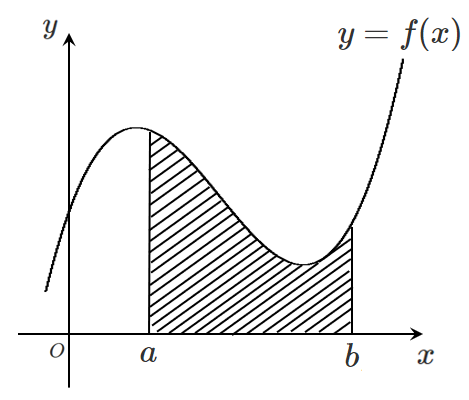
関数 $y=f(x)$ が $x$ 軸より上側にあるときは
$\displaystyle{S=\int_a^b f(x) dx}$
問題1
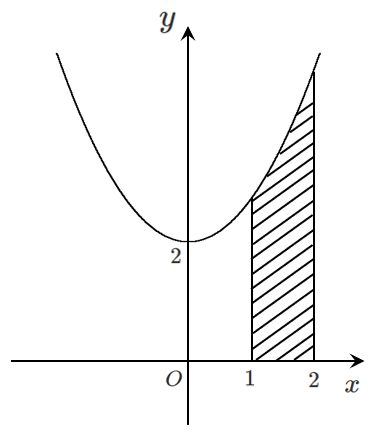
問題2
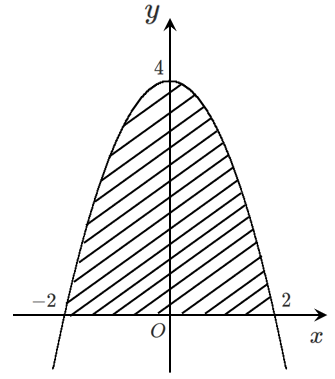
関数 $y=-x^2+4$ と $x$ 軸との共有点は
$y=0$ を代入して
$-x^2+4=0$
$x^2-4=0$
$(x-2)(x+2)=0$
$x=±2$
求める面積 $S$ は
\begin{align} S&=\int_{-2}^2 (-x^2+4) dx \\\\ &= \left[ -\frac{1}{3}x^3+4x \right]_{-2}^2 \\\\ &= -\frac{1}{3}\left\{2^3-(-2)^3\right\}+4\left\{2-(-2)\right\} \\\\ &= -\frac{16}{3}+16 \\\\ &= \frac{32}{3} \\\\ \end{align}$x$ 軸より下側の面積
$a≦x≦b$ において,$f(x)≦0$ のとき(関数 $y=f(x)$ が $x$ 軸より下側のとき)
関数 $y=f(x)$,2直線 $x=a$,$x=b$,$x$ 軸で囲まれる部分の面積 $S$ は
$\displaystyle{S=\int_a^b \left\{-f(x)\right\} dx}$
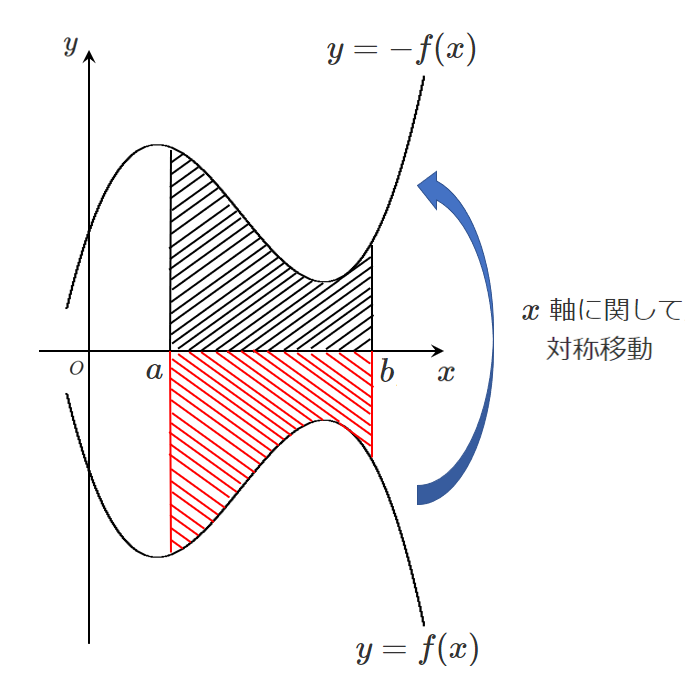
$x$ 軸より下側にある $y=f(x)$ と2直線 $x=a$,$x=b$,$x$ 軸で囲まれる部分の面積は
$y=f(x)$ のグラフを $x$ 軸に関して対称移動した $y=-f(x)$ と2直線 $x=a$,$x=b$,$x$ 軸で囲まれる部分の面積と等しいので
$S$$\displaystyle{=\int_a^b \left\{-f(x)\right\} dx}$
と表すことができる
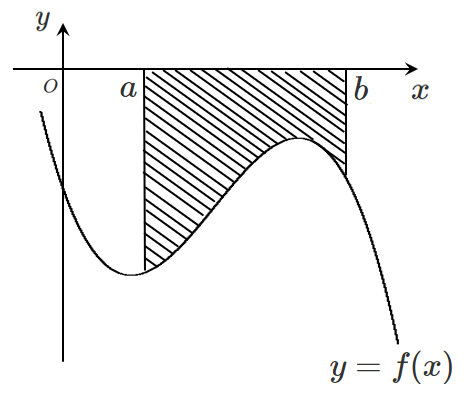
関数 $y=f(x)$ が $x$ 軸より下側にあるときは
$\displaystyle{S=\int_a^b \left\{-f(x)\right\} dx}$

$x$ 軸より下側なら,マイナスをつけて定積分!
問題3
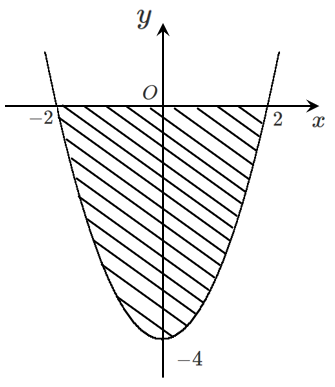
関数 $y=x^2-4$ と $x$ 軸との共有点は
$y=0$ を代入して
$x^2-4=0$
$(x-2)(x+2)=0$
$x=±2$
求める面積 $S$ は
\begin{align} S&=\int_{-2}^2 \left\{-(x^2-4)\right\} dx \\\\ &=\int_{-2}^2 (-x^2+4) dx \\\\ &= \left[ -\frac{1}{3}x^3+4x \right]_{-2}^2 \\\\ &= -\frac{1}{3}\left\{2^3-(-2)^3\right\}+4\left\{2-(-2)\right\} \\\\ &= -\frac{16}{3}+16 \\\\ &= \frac{32}{3} \\\\ \end{align}
定積分の計算ができれば,思ったより簡単に面積を求めることができるね!
まとめ
● 定積分と面積

関数 $y=f(x)$ が $x$ 軸より上側にあるときは
$\displaystyle{S=\int_a^b f(x) dx}$

関数 $y=f(x)$ が $x$ 軸より上側にあるときは
$\displaystyle{S=\int_a^b \left\{-f(x)\right\} dx}$

気を付けるのは, $x$ 軸より上側か下側かだけ!
下側なら,マイナスをつけて定積分!




コメント