対称式とは
対称式とは,どの2つの変数を変換しても変わらない多項式のことです。
例えば,$x^2+y^2$ は $x$ と $y$ を変換すると,$y^2+x^2$ となり,
$x$ と $y$ を変換しても変わらない多項式であるといえるため,$x^2+y^2$ は対称式です。
対称式の中でも,特に $x+y$,$xy$ のことを基本対称式といいます。
対称式は,基本対称式で表すことができます。
2変数の対称式の公式
2変数の対称式に関する問題
(1) $x+y$ (2) $xy$ (3) $x^2+y^2$
(4) $x^3+y^3$ (5) $x^5+y^5$
(1) $\displaystyle{x=\frac{2}{\sqrt{5}+\sqrt{3}}=\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}=\sqrt{5}-\sqrt{3}}$
$\displaystyle{y=\frac{2}{\sqrt{5}-\sqrt{3}}=\frac{2(\sqrt{5}+\sqrt{3})}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}=\sqrt{5}+\sqrt{3}}$
$\displaystyle{x+y=(\sqrt{5}-\sqrt{3})+(\sqrt{5}+\sqrt{3})=2\sqrt{5}}$
(2) $\displaystyle{xy=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)=2}$
(3) $x^2+y^2=(x+y)^2-2xy=(2\sqrt{5})^2-2\cdot2=16$
(4) $x^3+y^3=(x+y)^3-3xy(x+y)=(2\sqrt{5})^3-3\cdot2\cdot2\sqrt{5}=28\sqrt{5}$
(5) $x^5+y^5=(x^2+y^2)(x^3+y^3)-(xy)^2(x+y)$
$=16\cdot28\sqrt{5}-2^2\cdot2\sqrt{5}=440\sqrt{5}$
(1) $\displaystyle{x^2+\frac{1}{x^2}}$ (2) $\displaystyle{x^3+\frac{1}{x^3}}$
(3) $\displaystyle{x^4+\frac{1}{x^4}}$ (4) $\displaystyle{x-\frac{1}{x}}$
(1) $\displaystyle{x^2+\frac{1}{x^2}=\left(x+\frac{1}{x}\right)^2-2\cdot x\cdot\frac{1}{x}=3^2-2=7}$
(2) $\displaystyle{x^3+\frac{1}{x^3}=\left(x+\frac{1}{x}\right)^3-3\cdot x\cdot\frac{1}{x}\left(x+\frac{1}{x}\right)=3^3-3\cdot3=18}$
(3) $\displaystyle{x^4+\frac{1}{x^4}=\left(x^2+\frac{1}{x^2}\right)^2-2\cdot x^2\cdot\frac{1}{x^2}=7^2-2=47}$
(4) $\displaystyle{\left(x-\frac{1}{x}\right)^2=x^2-2\cdot x\cdot\frac{1}{x}+\frac{1}{x^2}=7-2=5}$
よって, $\displaystyle{x-\frac{1}{x}=\pm\sqrt{5}}$
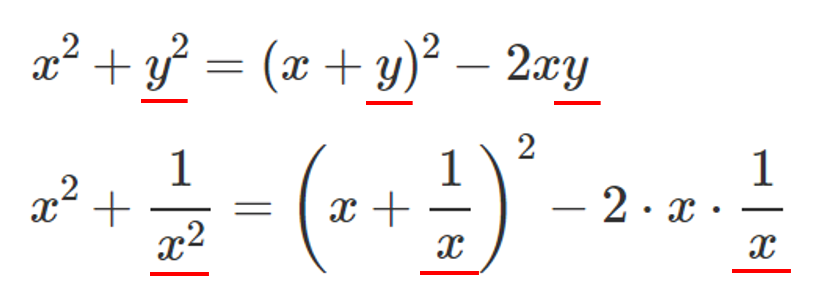

$y$ を $\displaystyle{\frac{1}{x}}$ と置き換えて考えるだけだね!

この式も覚えておくと便利だよ!
この公式を用いると $x+y$,$xy$ の値から $x-y$ の値を計算できます。
※ちなみに,$x-y$ は対称式ではありません
n乗の和を基本対称式で表す

$n-2$,$n-1$ の場合が求まれば,$n$ の場合 $x^n+y^n$ が求まるよ!
🔵整数部分の求め方をわかりやすく解説
🔵小数部分の求め方をわかりやすく解説
🔵二重根号のはずし方をわかりやすく解説
🔵場合分けによる絶対値記号のはずし方を解説
🔵√A²=|A| 間違える人がとても多い公式を解説
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント