高校数学Ⅱの【三角関数】で学ぶ『弧度法』について解説!
角度は,度(°)を単位とする『度数法』が基本でしたが,
三角関数の単元から『弧度法』という角度の表し方を学びます!
この投稿を見れば,『弧度法』の理解はバッチリ!
角度の表し方

角度の表し方は2種類あるよ!
度数法 … 度(°)を単位とした角度の表し方
弧度法 … 弧の長さを用いた角度の表し方

今までは「度数法」で角度を表していたね!
度数法

なじみのある度数法について詳しくみてみよう!
1周を $360^\circ$ にした理由は
・1年が $365$ 日だから
(当時は1年が $360$ 日くらいだった)
・約数が多いから
$1,2,3,4,5,6,8,9,10,\cdots$
といった理由が挙げられる

昔の人が1周を $360^\circ$ と決めただけで,数字的に深い意味は特にないのが度数法!
弧度法

弧の長さに着目した角度の表し方が「弧度法」!
単位は『ラジアン』!
弧度法の定義と単位
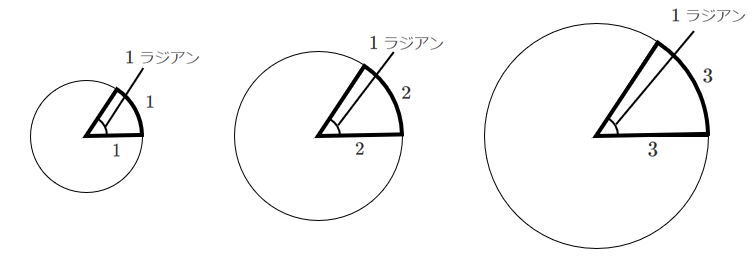
半径を $1$ のときの弧の長さが $1$ である中心角
半径を $2$ のときの弧の長さが $2$ である中心角
半径を $3$ のときの弧の長さが $3$ である中心角
円は必ず相似になるので,すべて等しい角度になる
これを $1$ ラジアン([rad]と書くこともある)とする
これが弧度法における $1$ の定義
円の半径を1で考える

半径が変わると考えにくいので,半径を $1$ に固定して考えてみよう!
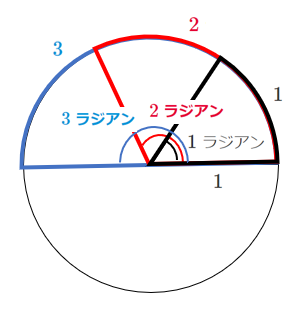
半径を $1$ にすることで
(弧の長さ)=(角度)で表せる
弧の長さが $1$ なら $1$ ラジアン
弧の長さが $2$ なら $2$ ラジアン
弧の長さが $3$ なら $3$ ラジアン
弧度法における1周

弧度法における1周は何ラジアンか考えてみよう!
半径を $1$ にしたときの1周
すなわち 円周の長さが弧度法における1周
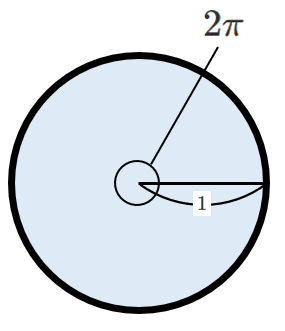
半径 $1$ の円周は $2\pi$ より
弧度法における1周は $2\pi$ ラジアン
半周を基準で考える
1周が $2\pi$ ラジアンなので
半周はその半分の $\pi$ ラジアン
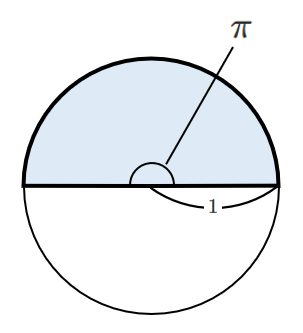
度数法の $180^\circ$ が
弧度法の $\pi$ ラジアン
90°
$180^\circ$ を $\displaystyle{\frac{1}{2}}$ 倍にしたのが $90^\circ$
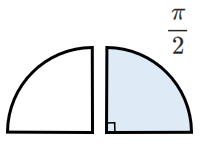
$\pi$ $[rad]$ を $\displaystyle{\frac{1}{2}}$ 倍にすると $\displaystyle{\frac{\pi}{2}}$
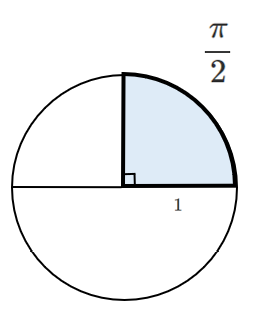

半分のパイを2等分したのが $\displaystyle{\frac{\pi}{2}}$ と考えると簡単!
60°
$180^\circ$ を $\displaystyle{\frac{1}{3}}$ 倍にしたのが $60^\circ$
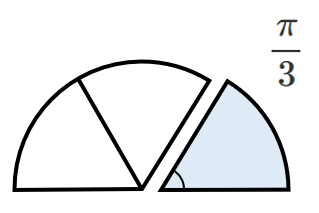
$\pi$ $[rad]$ を $\displaystyle{\frac{1}{3}}$ 倍にすると $\displaystyle{\frac{\pi}{3}}$
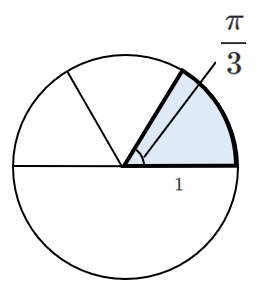

半分のパイを3等分したのが $\displaystyle{\frac{\pi}{3}}$ と考えると簡単!
45°
$180^\circ$ を $\displaystyle{\frac{1}{4}}$ 倍にしたのが $45^\circ$
$\pi$ $[rad]$ を $\displaystyle{\frac{1}{4}}$ 倍にすると $\displaystyle{\frac{\pi}{4}}$
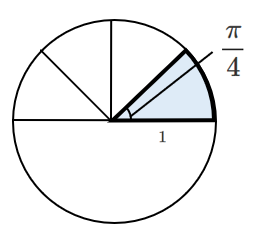

半分のパイを4等分したのが $\displaystyle{\frac{\pi}{4}}$ と考えると簡単!

30°
$180^\circ$ を $\displaystyle{\frac{1}{6}}$ 倍にしたのが $30^\circ$
$\pi$ $[rad]$ を $\displaystyle{\frac{1}{6}}$ 倍にすると $\displaystyle{\frac{\pi}{6}}$
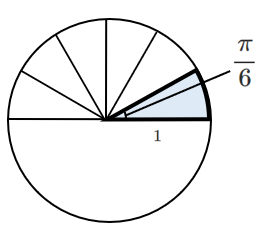

半分のパイを6等分したのが $\displaystyle{\frac{\pi}{6}}$ と考えると簡単!

弧度法まとめ
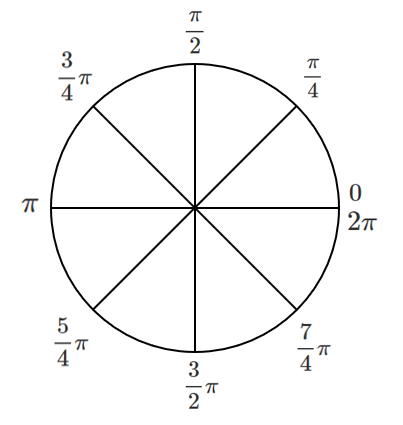
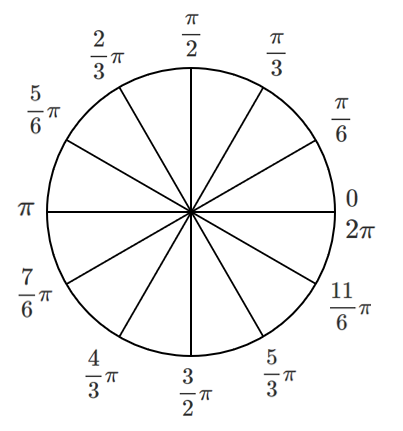
$\displaystyle{\frac{\pi}{2}}$,$\displaystyle{\frac{\pi}{3}}$,$\displaystyle{\frac{\pi}{4}}$,$\displaystyle{\frac{\pi}{6}}$ が何個集まってできた角なのかを考えると簡単
例
$150^\circ$ は $30^\circ$ が5個
すなわち $\displaystyle{\frac{\pi}{6}}$ が5個なので $\displaystyle{\frac{5}{6}\pi}$
度数法と弧度法の表
| 度数法 | 弧度法 |
| $0^\circ$ | $0$ |
| $30^\circ$ | $\displaystyle{\frac{\pi}{6}}$ |
| $45^\circ$ | $\displaystyle{\frac{\pi}{4}}$ |
| $60^\circ$ | $\displaystyle{\frac{\pi}{3}}$ |
| $90^\circ$ | $\displaystyle{\frac{\pi}{2}}$ |
| $120^\circ$ | $\displaystyle{\frac{2}{3}\pi}$ |
| $135^\circ$ | $\displaystyle{\frac{3}{4}\pi}$ |
| $150^\circ$ | $\displaystyle{\frac{5}{6}\pi}$ |
| $180^\circ$ | $\pi$ |
| $210^\circ$ | $\displaystyle{\frac{7}{6}\pi}$ |
| $225^\circ$ | $\displaystyle{\frac{5}{4}\pi}$ |
| $240^\circ$ | $\displaystyle{\frac{4}{3}\pi}$ |
| $270^\circ$ | $\displaystyle{\frac{3}{2}\pi}$ |
| $300^\circ$ | $\displaystyle{\frac{5}{3}\pi}$ |
| $315^\circ$ | $\displaystyle{\frac{7}{4}\pi}$ |
| $330^\circ$ | $\displaystyle{\frac{11}{6}\pi}$ |
| $360^\circ$ | $2\pi$ |
扇形の弧の長さと面積
角を弧度法で表すことで,扇形の弧の長さと面積を簡単に求めることができます!
半径 $r$,中心角 $\theta$(弧度法)の扇形の弧の長さを $l$,面積を $S$ とすると
$l=r\theta$ , $\displaystyle{S=\frac{1}{2}r^2\theta=\frac{1}{2}lr}$
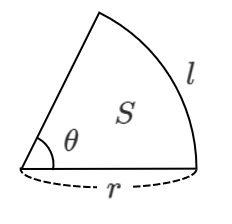
【証明】
円において,扇形の弧の長さと面積はともに中心角の大きさに比例するので
$l:2\pi r=\theta:2\pi$ すなわち $\displaystyle{l=\frac{2\pi r\theta}{2\pi}=r\theta}$
$S:\pi r^2=\theta:2\pi$ すなわち $\displaystyle{S=\frac{\pi r^2 \theta}{2\pi}=\frac{1}{2}r^2\theta}$
さらに $\displaystyle{S=\frac{1}{2}r\theta\cdot r=\frac{1}{2}lr}$
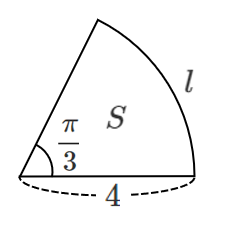
$\displaystyle{l=4\cdot\frac{\pi}{3}=\frac{4}{3}\pi}$
$\displaystyle{S=\frac{1}{2}\cdot4^2\cdot\frac{\pi}{3}=\frac{8}{3}\pi}$
まとめ
● 度数法の定義
1周を $360^\circ$ としたときの $\displaystyle{\frac{1}{360}}$ が $1^\circ$
● 弧度法の定義
半径と等しい弧に対する中心角の大きさを $1$ ラジアン
● 弧度法における角
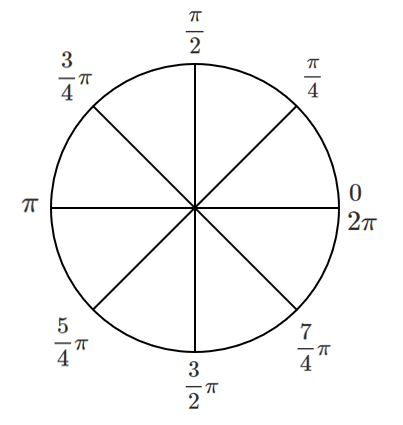
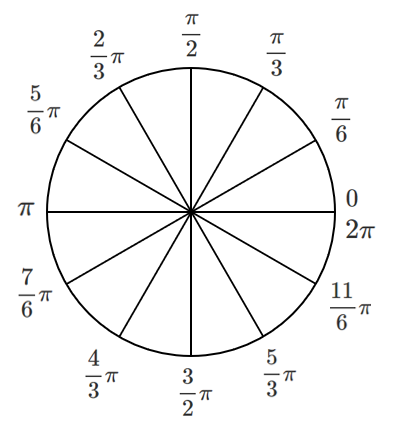

暗記するのではなく,半周が $\pi$ を基準に考えるようにしよう!




コメント