「必要条件・十分条件はややこしい!どっちがどっちか分からなくなってしまう…」
そのような悩みを持つ人がとても多いです!
逆に,きちんと理解して解けるようになれば,他の人と差をつけることができます!
この投稿では,誰でもわかる必要条件・十分条件の判別方法と覚え方を説明します!
最後まで読んで,必要条件・十分条件を完璧にマスターしましょう!
必要条件・十分条件とは

教科書にも書いてある「必要条件・十分条件」の説明はこれ!
● $p$ は $q$ であるための十分条件
● $q$ は $p$ であるための必要条件

これは教科書で見たけど,よくわからない…

これでは難しいので,わかりやすく解説するよ!
必要条件・十分条件の判定をするには,真偽の判定が重要になる!
まずは真偽の判定から学ぼう!
真偽の判定
「命題 $p\Longrightarrow q$ は真である」ことは
「 $p$ を満たすものはすべて $q$ を満たす 」こと
このことを集合で表してみる
条件 $p$ を満たす全体の集合を $P$
条件 $q$ を満たす全体の集合を $Q$
とすると
「命題 $p\Longrightarrow q$ は真である」ことは
「 $P$ の要素はすべて $Q$ の要素になる 」こと
すなわち $P⊂Q$( $P$ は $Q$ に含まれる)
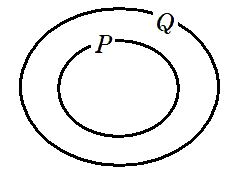
「$⊂$」の記号が分からないときはこれ↓

集合の大小関係で,真偽の判定ができるってことかな?

その通り!
具体例を見てみよう!
三毛猫 $\Longrightarrow$ 猫
猫 $\Longrightarrow$ 三毛猫
「三毛猫」と「猫」を集合で考えると
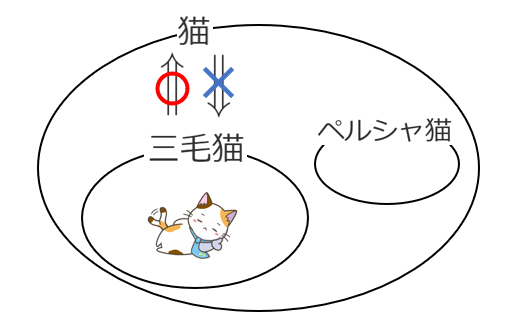
「三毛猫」という集合が「猫」という集合に含まれている
三毛猫 $\Longrightarrow$ 猫 は 真
猫 $\Longrightarrow$ 三毛猫 は 偽
反例は「ペルシャ猫」
詳しく学びたい人はこれ↓

必要条件・十分条件の判別方法

「○」は真,「×」は偽
「大」と「小」は集合の大小関係
(2) $x^2=1$ であることは,$x=1$ であるための( )条件
(1) $a$ が $4$ の倍数であることは,$a$ が $2$ の倍数であるための( )条件
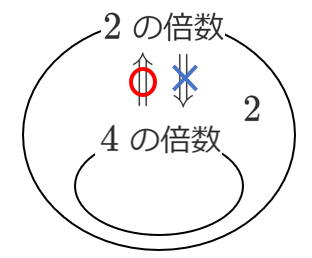
「$4$ の倍数」の集合が「$2$ の倍数」の集合に含まれているので,
$a$ が $4$ の倍数 $\Longrightarrow$ $a$ が $2$ の倍数 は 真
$a$ が $4$ の倍数 $\Longleftarrow$ $a$ が $2$ の倍数 は 偽(反例:$a=2$)
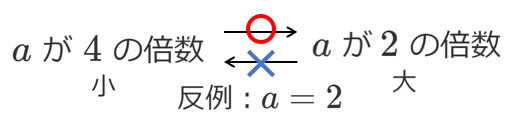
$a$ が $4$ の倍数であることは,$a$ が $2$ の倍数であるための十分条件
(2) $x^2=1$ であることは,$x=1$ であるための( )条件
$x^2=1$ を解くと,$x=\pm1$
$x=\pm1$ $\Longrightarrow$ $x=1$ は 偽(反例:$x=-1$)
$x=\pm1$ $\Longleftarrow$ $x=1$ は 真

$x^2=1$ であることは,$x=1$ であるための必要条件
必要条件と十分条件の覚え方

必要条件と十分条件の矢印の方向を忘れちゃう…
何か覚え方はないのかな?

「主語から見て矢印をお金の流れと考える」
のが簡単な覚え方だよ!


お金の流れで考えると簡単に覚えられるね!
必要十分条件
必要十分条件とは、必要条件でも十分条件でもある条件のことです。
つまり,「$p \Longrightarrow q$」と「$q \Longrightarrow p$」がともに真であれば,$p$ と $q$ は互いに十分条件かつ必要条件となります。

$p$ と$q$ が必要十分条件であるとき,$p$ と $q$ は同値であるといいます。
$p$ と $q$ が同値であるとき, $p \Longleftrightarrow q$ と表します。
必要条件でも十分条件でもない
最後に,「必要条件でも十分条件でもない」場合について説明します。

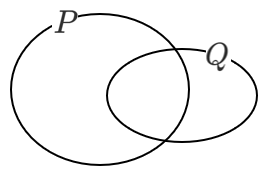
集合で考えて,以下のように包含関係が成り立たないとき,「必要条件でも十分条件でもない」という選択肢になります。
問題演習
(1) $x=1$ は,$x$ が奇数であるための( )
(2) $x>0$ は,$x>1$ であるための( )
(3) $x^2+y^2=0$ は,$x=y=0$ であるための( )
(4) $a$ が素数であることは,$a$ が奇数であるための( )
(1) $x=1$ は,$x$ が奇数であるための( )
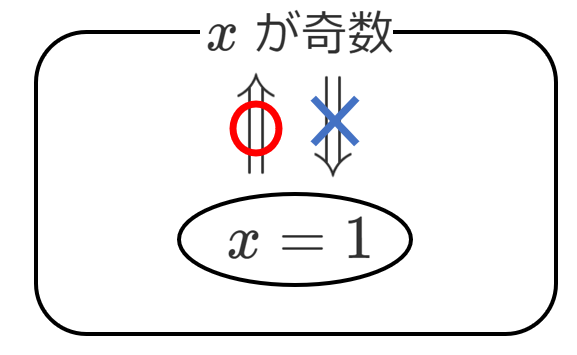

$x=1$ は,$x$ が奇数であるための十分条件
(2) $x>0$ は,$x>1$ であるための( )
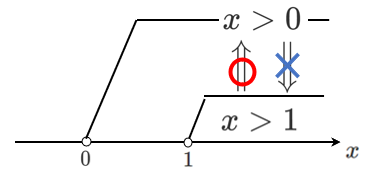

$x>0$ は,$x>1$ であるための必要条件
(3) $x^2+y^2=0$ は,$x=y=0$ であるための( )

$x^2+y^2=0$ は,$x=y=0$ であるための必要十分条件
(4) $a$ が素数であることは,$a$ が奇数であるための( )
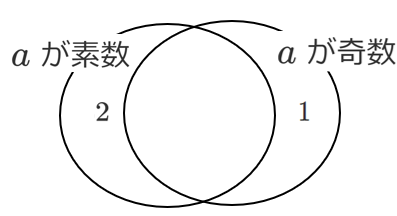

$a$ が素数であることは,$a$ が奇数であるための必要条件でも十分条件でもない
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!





コメント