
指数関数を学ぶ前の準備!
指数の拡張について学ぼう!
指数法則

指数を学ぶ上での基本!
指数法則をおさえよう!
指数とは


右肩につく数のことを「指数」と呼ぶよ!
指数法則
$a>0$,$b>0$ で,$r$,$s$ が実数とする
1 $a^r\times a^s=a^{r+s}$ 2 $\displaystyle{\frac{a^r}{a^s}=a^{r-s}}$
3 $\left(a^r\right)^s=a^{rs}$ 4 $(ab)^r=a^r b^r$

1と2は間違えやすいので,分からなくなったら具体例を用いて考えよう!
$2^2\times2^3=(2\times2)\times(2\times2\times2)=2^5$
$2$ が $2$ 個と,$2$ が $3$ 個で合計 $5$ 個
$2+3=5$
つまり $2^2\times2^3=2^{2+3}=2^5$
$(2^2)^3=(2\times2)\times(2\times2)\times(2\times2)=2^6$
$2$ が $2$ 個が $3$ セットで合計 $6$ 個
$2\times3=6$
つまり $(2^2)^3=2^{2\times3}=2^6$

「指数法則」は実数全体で成り立つことが知られているよ!
指数が整数

$2^{-1}$ や $2^{-2}$ が何になるか考えよう!
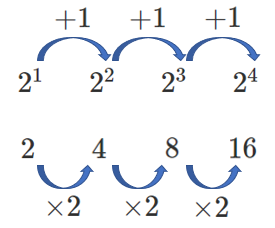
$2^□$ は指数が $+1$ されるごとに $\times2$ になる
これを拡張すると以下のようになる
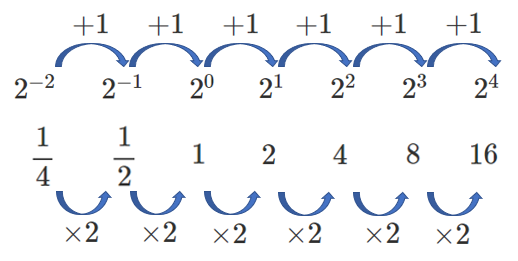
同様に考えると $\displaystyle{2^{-3}=\frac{1}{8}}$
$\displaystyle{2^{-4}=\frac{1}{16}}$ である
$\displaystyle{2^{-3}=\frac{1}{2^3}}$
$\displaystyle{2^{-4}=\frac{1}{2^4}}$
であることから以下のことがいえる
$a≠0$ で,$n$ は正の整数とする
$\displaystyle{a^{-n}=\frac{1}{a^n}}$ $a^0=1$
$n$ 乗根
<$n$ 乗根の例>
$4$ の $2$ 乗根(平方根) …… $2$ 乗すると $4$ になる数 $±2$
$8$ の $3$ 乗根 …… $3$ 乗すると $8$ になる数 $2$
$16$ の $4$ 乗根 …… $4$ 乗すると $16$ になる数 $±2$

$n$ 乗根が整数ではない数になったらどうやって表すの?

平方根と同様に,$\sqrt{ }$ を使って表すよ!
正の数 $a$ の $n$ 乗根のうち,正であるものを $\sqrt[n]{a}$ で表す($n$ 乗根 $a$ と読む)
$n=2$ のときは $2$ を省略して $\sqrt{a}$ と表す
<$\sqrt[n]{a}$ の例>
$2$ の $2$ 乗根(平方根) …… $2$ 乗したら $2$ になる数 $±\sqrt{2}$
$2$ の $3$ 乗根 …… $3$ 乗したら $2$ になる数 $\sqrt[3]{2}$
$2$ の $4$ 乗根 …… $4$ 乗したら $2$ になる数 $±\sqrt[4]{2}$
次の数を簡単にせよ。
(1) $\sqrt{16}$ (2) $\sqrt[3]{8}$ (3) $\sqrt[4]{81}$
(1) $\sqrt{16}$
$2$ 乗したら $16$ になる正の数なので
$\sqrt{16}=4$
(2) $\sqrt[3]{8}$
$3$ 乗したら $8$ になる正の数なので
$\sqrt[3]{8}=2$
(3) $\sqrt[4]{81}$
$4$ 乗したら $81$ になる正の数なので
$\sqrt[4]{81}=3$

式でみると,このように考えられる!
$\sqrt{16}=\sqrt{4^2}=4$
$\sqrt[3]{8}=\sqrt[3]{2^3}=2$
$\sqrt[4]{81}=\sqrt[4]{3^4}=3$
$\sqrt[n]{a}$ について,以下の性質がいえる
$\sqrt{2}$ は $2$ 乗したら $2$ になる数なので
$(\sqrt{2})^2=2$ $\sqrt{2^2}=\sqrt{4}=2$
$\sqrt[3]{2}$ は $3$ 乗したら $2$ になる数なので
$(\sqrt[3]{2})^3=2$ $\sqrt[3]{2^3}=\sqrt[3]{8}=2$
$\sqrt[4]{2}$ は $4$ 乗したら $2$ になる数なので
$(\sqrt[4]{2})^4=2$ $\sqrt[4]{2^4}=\sqrt[4]{16}=2$

$\sqrt[n]{ }$ の中に $○^n$ があれば,$\sqrt[n]{ }$ がとれる!
$(\sqrt[n]{a})^n=a$,$\sqrt[n]{a^n}=a$ より,
$(\sqrt[n]{a})^n=\sqrt[n]{a^n}$
が成り立つ
同様に考えると
$(\sqrt[n]{a})^m=\sqrt[n]{a^m}$
指数が有理数

「有理数」とは分数で表される数のこと!
指数が「有理数」になるときについて考えよう!
$a^{\frac{1}{n}}$

$a^{\frac{1}{2}}$ はどんな数なのかな?

$2$ 乗してみたら,どんな数か分かるよ!
指数法則 $a^r\times a^s=a^{r\times s}$ を用いて,$2^{\frac{1}{2}}$ を $2$ 乗してみると
$(2^{\frac{1}{2}})^2=2^{\frac{1}{2}\times2}=2^1=2$
$2^{\frac{1}{2}}$ は $2$ 乗したら $2$ になる正の数であることがわかる
$2$ 乗して $2$ になる正の数は $\sqrt{2}$ であるので
$2^{\frac{1}{2}}=\sqrt{2}$

$\sqrt[3]{2}$ がどのような数になるか調べたいときはどうする?

$3$ 乗してみたらいいのかな?
指数法則 $a^r\times a^s=a^{r\times s}$ を用いて,$2^{\frac{1}{3}}$ を $3$ 乗してみると
$(2^{\frac{1}{3}})^3=2^{\frac{1}{3}\times3}=2^1=2$
$2^{\frac{1}{3}}$ は $3$ 乗したら $2$ になる正の数であることがわかる
$3$ 乗して $2$ になる正の数は $\sqrt[3]{2}$ であるので
$2^{\frac{1}{3}}=\sqrt[3]{2}$
$a>0$ で,$n$ は正の整数とする
$a^{\frac{1}{n}}=\sqrt[n]{a}$
$a^{\frac{m}{n}}$

$2^{\frac{1}{3}}=\sqrt[3]{2}$ を用いて,$2^{\frac{2}{3}}$ について考えてみよう!
指数法則 $a^r\times a^s=a^{r\times s}$,$2^{\frac{1}{3}}=\sqrt[3]{2}$, $(\sqrt[n]{a})^m=\sqrt[n]{a^m}$ を用いて
$2^{\frac{2}{3}}=2^{\frac{1}{3}\times2}=(2^{\frac{1}{3}})^2=(\sqrt[3]{2})^2=\sqrt[3]{2^2}$
よって
$2^{\frac{2}{3}}=\sqrt[3]{2^2}$

以上より,次のことがいえるよ!
$a>0$ で,$m$,$n$ は正の整数とする
$a^{\frac{m}{n}}=\sqrt[n]{a^m}$
問題
次の□に適する数を求めよ。
(1) $3^{\frac{1}{4}}=\sqrt[□]{□}$ (2) $2^{\frac{3}{4}}=\sqrt[□]{□^□}$ (3) $\displaystyle{4^{-\frac{2}{3}}=\frac{1}{\sqrt[□]{□^□}}}$
(4) $\sqrt[3]{5}=□^{\frac{□}{□}}$ (5) $\sqrt[5]{16}=\sqrt[5]{2^□}=2^{\frac{□}{□}}$
(1) $3^{\frac{1}{4}}=\sqrt[□]{□}$
$3^{\frac{1}{4}}=\sqrt[4]{3}$
(2) $2^{\frac{3}{4}}=\sqrt[□]{□^□}$
$2^{\frac{3}{4}}=\sqrt[4]{2^3}$
(3) $\displaystyle{4^{-\frac{2}{3}}=\frac{1}{\sqrt[□]{□^□}}}$
$\displaystyle{4^{-\frac{2}{3}}=\frac{1}{\sqrt[3]{4^2}}}$
(4) $\sqrt[3]{5}=□^{\frac{□}{□}}$
$\sqrt[3]{5}=5^{\frac{1}{3}}$
(5) $\sqrt[5]{16}=\sqrt[□]{2^□}=2^{\frac{□}{□}}$
$\sqrt[5]{16}=\sqrt[5]{2^4}=2^{\frac{4}{5}}$

指数の基本をきちんと理解しよう!




コメント