
微分を用いて接線の方程式を求めよう!
接線
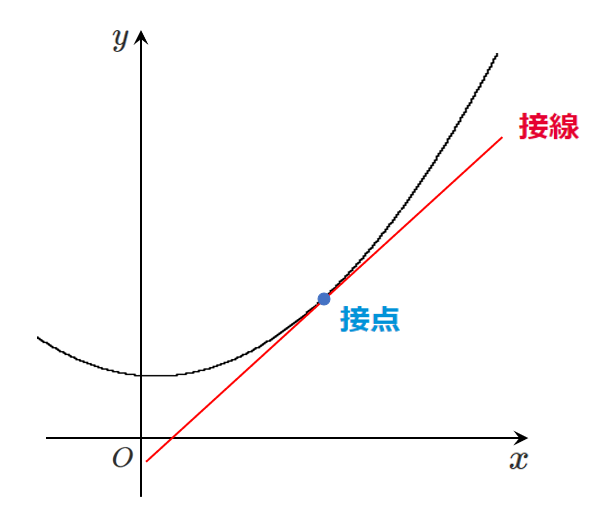
接線の傾きは微分係数
関数 $y=f(x)$ の $x=a$ における微分係数 $f'(a)$ は
関数 $y=f(x)$ のグラフ上の点 $A(a,f(a))$ における接線の傾きと等しい
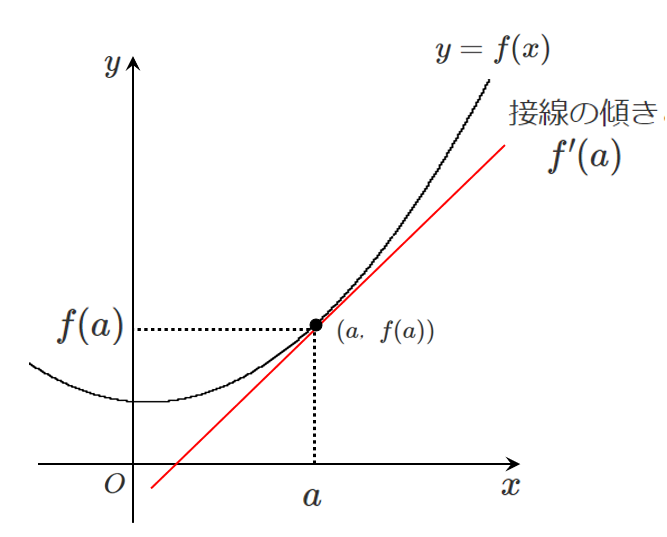
微分係数と接線の傾きの関係はこれ↓

微分係数の求め方

微分係数の定義式を用いれば微分係数は求まるけど,計算に時間がかかる!
以下の手順で微分係数を求めよう!
導関数の求め方はこれ↓
問題
関数 $f(x)$ の導関数を求めると
$f'(x)=2x+2$
$x=1$ における $f(x)$ の微分係数 $f'(1)$ は
$f'(1)=2\cdot1+2=4$

導関数を求めて代入すれば微分係数が求まるね!
接線の方程式(接点が与えられている)

接線は直線!
直線の方程式の求め方を復習しよう!
直線の方程式
傾き $m$,点 $(x_1,y_1)$ を通る直線の方程式は
$y-y_1=m(x-x_1)$

直線の方程式は「傾き」と「通る点」で求まる
だったね!
直線の方程式の復習はこれ↓

接線の方程式

接線の方程式は
「傾き」が微分係数
「通る点」が接点
で考えるのが基本!
「通る点」が接点
問題
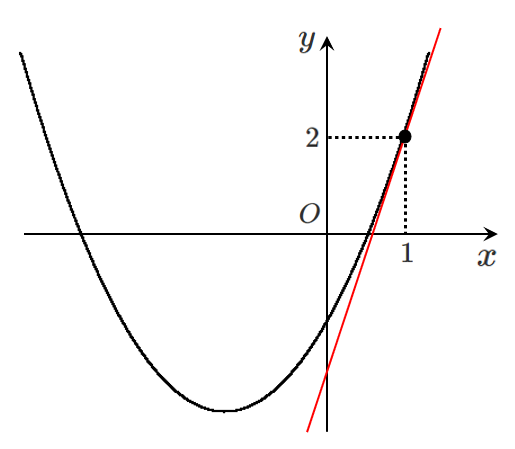
$f(x)$ の導関数は
$f'(x)=2x+2$
$(1,2)$ における接線の傾きは,$x=1$ における微分係数 $f'(1)$ なので
$f'(1)=2\cdot1+2=4$
求める接線は傾き $4$,点 $(1,2)$ を通る直線なので
$y-2=4(x-1)$
$y=4x-2$

接線も直線だから,「傾き」と「通る点」がキーワードだね!
まとめ
● 接線の傾きは微分係数
関数 $y=f(x)$ の $x=a$ における微分係数 $f'(a)$ は
関数 $y=f(x)$ のグラフ上の点 $A(a,f(a))$ における接線の傾きと等しい

● 直線の方程式
傾き $m$,点 $(x_1,y_1)$ を通る直線の方程式は
$y-y_1=m(x-x_1)$
● 接線の方程式
「傾き」が微分係数,「通る点」が接点
で直線の方程式を用いる

微分係数と接線の傾きの関係を理解して,直線の方程式を用いよう!




コメント