方べきの定理
$PA・PB=PC・PD$
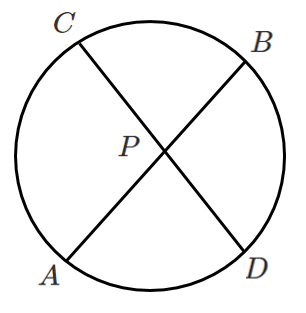
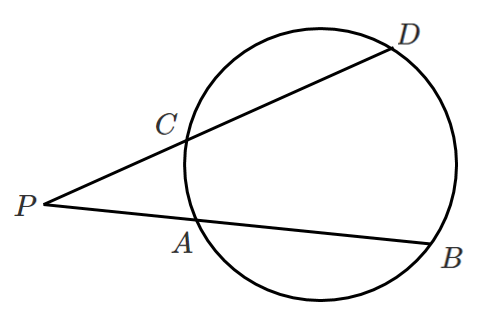
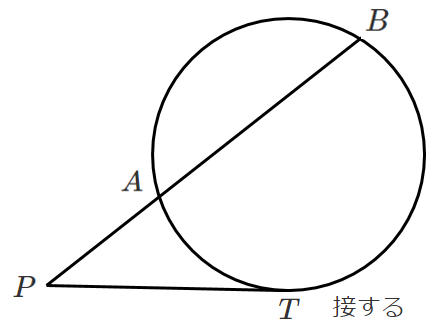

簡単にまとめるとこんな感じ!
$□\cdot□$$ = $$□\cdot□$
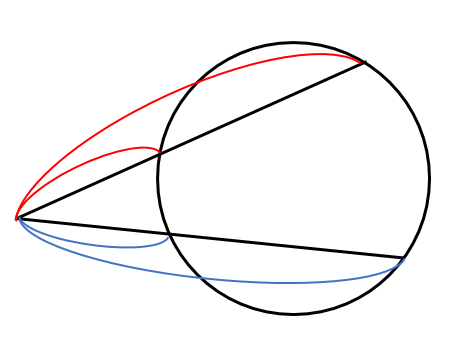
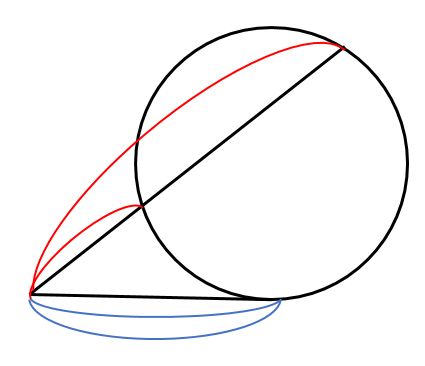

方べきの定理はこの3種類を使いこなせばいいんだね!
証明
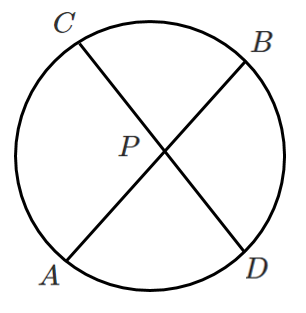
[証明]
$\triangle PAC$ と $\triangle PDB$ を考える
円周角の定理より
$\angle PAC=\angle PDB$
$\angle PCA=\angle PBD$
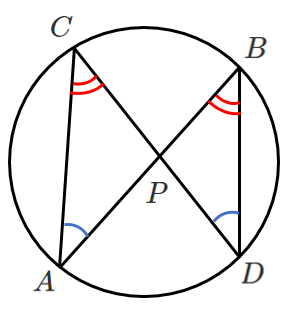
2組の角がそれぞれ等しいので
$\triangle PAC\backsim\triangle PDB$
したがって
$PA:PC=PD:PB$
これより
$PA・PB=PC・PD$
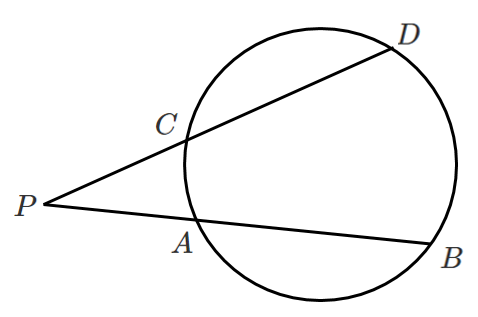
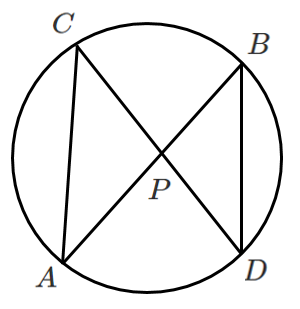
[証明]
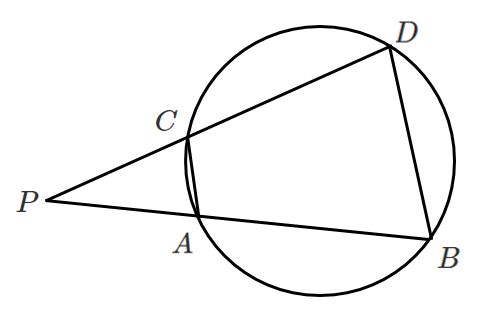
$\triangle PAC$ と $\triangle PDB$ を考える
円に内接する四角形の性質より
$\angle PAC=\angle PDB$
$\angle PCA=\angle PBD$
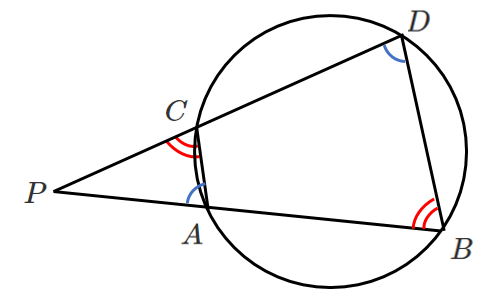
2組の角がそれぞれ等しいので
$\triangle PAC\backsim\triangle PDB$
したがって
$PA:PC=PD:PB$
これより
$PA・PB=PC・PD$
円に内接する四角形の性質はこれ↓

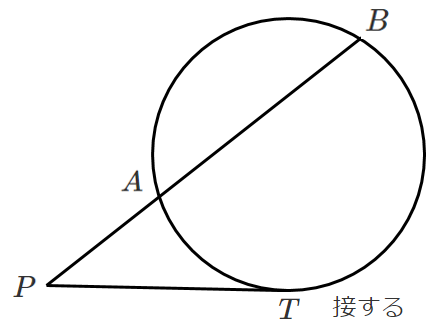
[証明]
下図のように円の中心 $O$,点 $C$,$D$ をとる
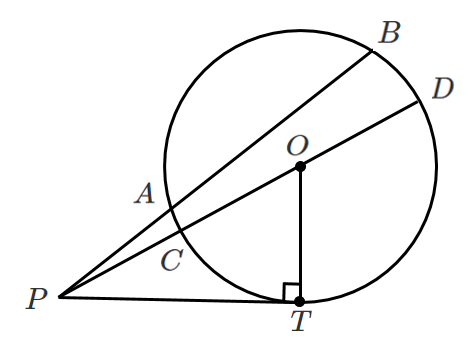
方べきの定理より
$PA・PB=PC・PD$
円の半径を $r$ とすると
$PC=PO-r$,$PD=PO+r$
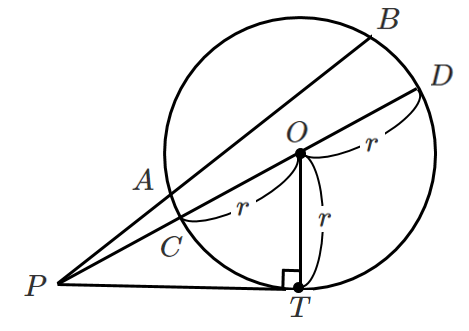
これより
$PA・PB=PC・PD=(PO-r)(PO+r)$
よって
$PA・PB=PO^2-r^2$
$\triangle OPT$ において三平方の定理より
$PT^2=PO^2-r^2$
したがって
$PA・PB=PT^2$
まとめ
● 方べきの定理
$□・□$$ = $$□・□$



問題
(1)
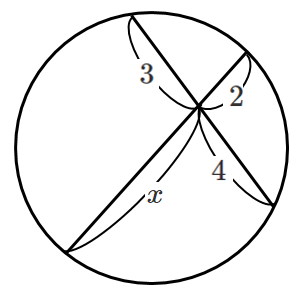
方べきの定理より
$x・2=3・4$
$x=6$
(2)
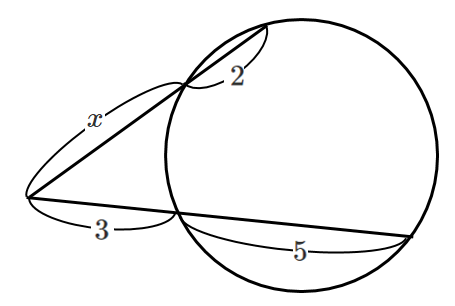
方べきの定理より
$x(x+2)=3・8$
$x^2+2x=24$
$x^2+2x-24=0$
$(x-4)(x+6)=0$
$x>0$ より $x=4$
(3)
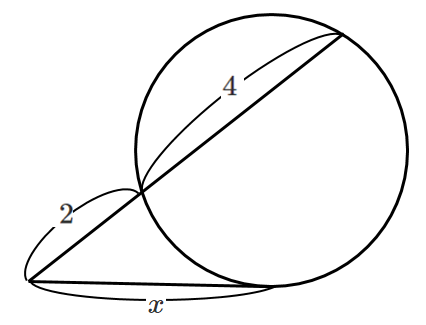
方べきの定理より
$x^2=2・6$
$x^2=12$
$x>0$ より $x=2\sqrt{3}$

3つの方べきの定理を使いこなそう!




コメント