
素因数分解を用いた最大公約数と最小公倍数の求め方と応用問題を解いてみよう!
最大公約数
約数
$24$ の正の約数
$1,2,3,4,6,8,12,24$
$24$ を割り切ることができる数
公約数

公約数とは共通する約数のこと!
$24$ と $36$ の正の公約数
$24$ の約数
$1,2,3,4,6,8,12,24$
$36$ の約数
$1,2,3,4,6,9,12,18,36$
公約数は
$1,2,3,4,6,12$
最大公約数

最大公約数は公約数の中で最大のもの!
$24$ と $36$ の正の公約数は
$1,2,3,4,6,12$
$24$ と $36$ の最大公約数は $12$

約数→公約数→最大公約数の順に理解しておこう!
最小公倍数
倍数
$12$ の正の倍数
$12,24,36,48,60,72,84,\cdots$
$12$ を整数倍したもの
公倍数

公倍数とは共通する倍数のこと!
$12$ と $16$ の正の公倍数
$12$ の約数
$12,24,36,48,60,72,84,96,\cdots$
$16$ の約数
$16,32,48,64,80,96,112,128,\cdots$
公倍数は
$48,96,144,\cdots$
最小公倍数

最小公倍数は公倍数の中で最小のもの!
$12$ と $16$ の正の公倍数は
$48,96,144,\cdots$
$12$ と $16$ の最大公約数は $48$

倍数→公倍数→最小公倍数の順に理解しておこう!
素因数分解を用いた求め方

最大公約数と最小公倍数を簡単に求める方法はこれ!
リンク

素因数分解を用いた求め方は応用しやすいので,きちんと確認しておこう!
素因数分解の復習はこれ↓

最大公約数の求め方
素因数分解をすると
$36=2^2・3^2$
$120=2^3・3^1・5^1$
最大公約数は共通する約数の中で最大のもの
共通する素因数で最大のもの $2^2・3^1=12$ が最大公約数
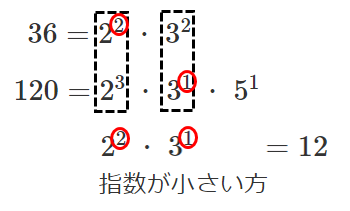

最大公約数は「指数が小さい方」をとる!
最小公倍数の求め方
素因数分解をすると
$36=2^2・3^2$
$120=2^3・3^1・5^1$
最小公倍数は共通する倍数の中で最小のもの
$2^2・3^2$ と $2^3・3^1・5^1$ の両方を因数にもつ $2^3・3^2・5^1=360$ が最小公倍数
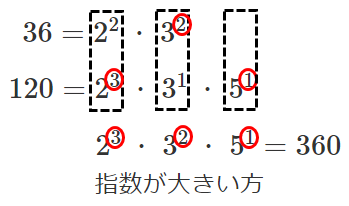

最小公倍数は「指数が大きい方」をとる!

ちなみに,3つ以上の数の最大公約数と最小公倍数も求め方は同じだよ!
最小公倍数からもとの数を求める
素因数分解すると
$12=2^2・3^1$
$180=2^2・3^2・5^1$
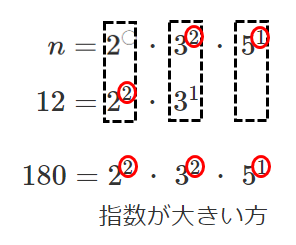
$n$ は $3^2$ と $5^1$ を素因数にもつ必要がある
素因数 $2$ については
もたない
$2^1$ をもつ
$2^2$ をもつ
のいずれかであるので
$n=3^2・5^1,2^1・3^2・5^1,2^2・3^2・5^1$
すなわち $n=45,90,180$

素因数分解して並べてみると分かりやすいね!
まとめ
● 素因数分解を用いた最大公約数と最小公倍数の求め方
素因数分解をして上下に並べて
・最大公約数は「指数が小さい方」
・最小公倍数は「指数が大きい方」
をとる
問題
素因数分解をすると
$24=2^3・3^1$
$180=2^2・3^2・5^1$
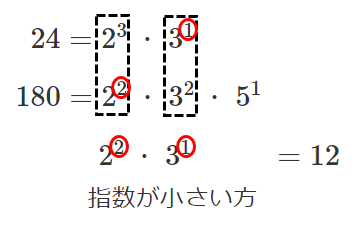
最大公約数は $2^2・3^1=12$
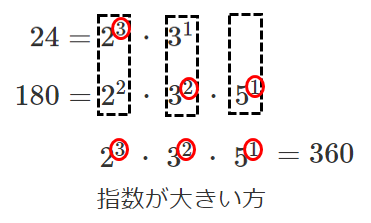
最小公倍数は $2^3・3^2・5^1=360$
素因数分解をすると
$24=2^3・3^1$
$90=2^1・3^2・5^1$
$126=2^1・3^2・7^1$
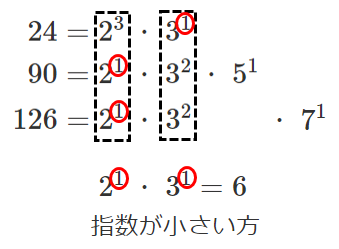
最大公約数は $2^1・3^1=6$
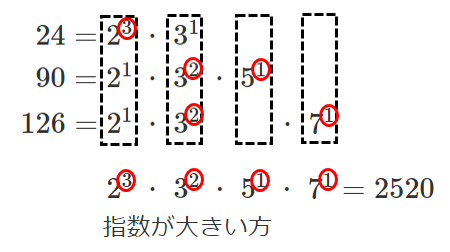
最小公倍数は $2^3・3^2・5^1・7^1=2520$
素因数分解すると
$18=2^1・3^2$
$180=2^2・3^2・5^1$
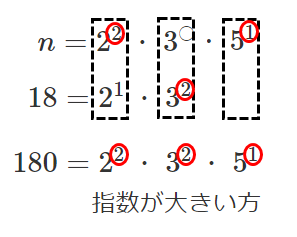
$n$ は $2^2$ と $5^1$ を素因数にもつ必要がある
素因数 $3$ については
もたない
$3^1$ をもつ
$3^2$ をもつ
のいずれかであるので
$n=2^2・5^1,2^2・3^1・5^1,2^2・3^2・5^1$
すなわち $n=20,60,180$

素因数分解を用いると応用問題にも対応できるね!




コメント