
極値の条件から関数の決定をする問題を解いてみよう!
$x=a$ で極値をとるための条件

極大・極小の増減表における共通点をみてみよう!
導関数 $f'(x)$ を求めると
$f'(x)=3x^2-6x=3x(x-2)$
$f'(x)=0$ を求めると
$3x(x-2)=0$
$x=0,2$
$f'(x)$ のグラフをかくと
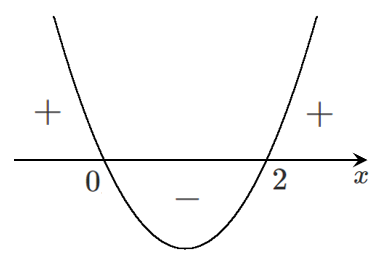
増減表をかくと
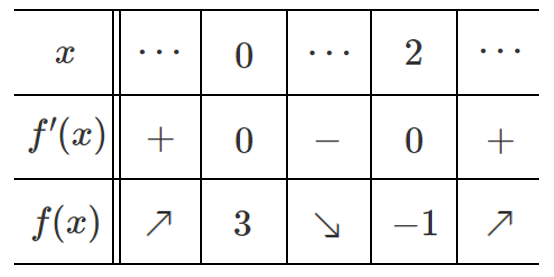
したがって
$x=0$ で極大値 $3$
$x=2$ で極小値 $-1$
このとき
$x=0,2$ における $f'(x)$ の値は $0$ になっている

極大・極小をとるときの $f'(x)$ の値は必ず $0$ になっているね!

極大・極小に関する問題を解いていると,そのような共通点に気が付くね!

逆に,
「$f'(a)=0$ ならば,関数 $f(x)$ が $x=a$ で極値をとる」
は成り立たないことに注意しよう!

どういうこと?

$f(x)=x^3$ を例に考えてみよう!
導関数 $f'(x)$ を求めると
$f'(x)=3x^2$
$f'(x)=0$ を求めると
$3x^2=0$
$x=0$
$f'(x)$ のグラフをかくと
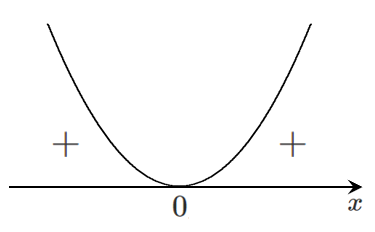
増減表をかくと
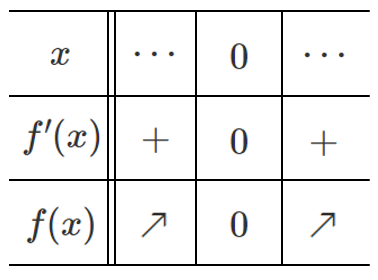
関数 $f(x)$ は常に増加する
つまり,増減が入れかわらないので
$f(x)$ は極値をもたない
関数 $f(x)=x^3$ は
$f'(0)=0$ であるが,$x=0$ で極値をもたない
ことがわかる

逆が成り立たないことを理解しておく必要があるね!
問題
定数 $a$,$b$ の値を求めよ。また,極小値を求めよ。
関数 $f(x)=x^3+ax^2+bx$ を微分すると
$f'(x)=3x^2+2ax+b$
関数 $f(x)$ が $x=1$ で極大値 $4$ をとるとき
$f'(1)=0$,$f(1)=4$
$f'(1)=0$ より
$3\cdot1^2+2a\cdot1+b=0$
$2a+b=-3$ $\cdots\cdots$ ①
$f(1)=4$ より
$1^3+a\cdot1^2+b\cdot1=4$
$a+b=3$ $\cdots\cdots$ ②
①,②を解いて
$a=-6$,$b=9$
このとき
$f(x)=x^3-6x^2+9x$
$f'(x)=3x^2-12x+9=3(x^2-4x+3)=3(x-1)(x-3)$
$f'(x)=0$ のとき
$3(x-1)(x-3)=0$
$x=1,3$
$f'(x)$ のグラフは
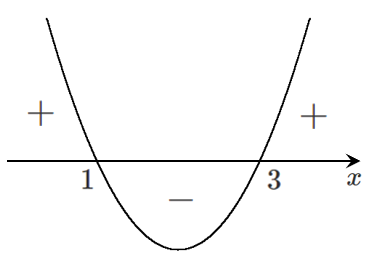
増減表をかくと
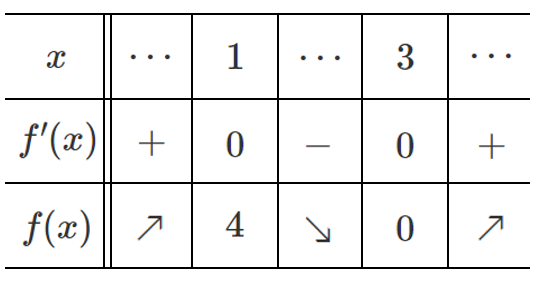
$x=3$ で極小値 $0$ をとる

$f'(1)=0$ であっても $f(x)$ が $x=1$ で極大値をとるとは限らないため,増減表で $f(x)$ が $x=1$ で極大値 $4$ をとることを確認しよう!

「$f'(a)=0$ ならば,$x=a$ で極値をもつ」が成り立たないからだね!
答えが出ても,忘れずに増減表を書いて確認しよう!
まとめ
● 極値の条件から関数の決定
関数 $f(x)$ が $x=a$ で極値をもつならば,$f'(x)=0$ である
逆「$f'(a)=0$ ならば,関数 $f(x)$ が $x=a$ で極値をもつ」は成り立たない

よく出題されるので,きちんとおさえておこう!




コメント