高校数学Ⅰの『図形と計量』で頻出の『正弦(sin)が与えられている三角形の最大角を求める問題』をわかりやすく解説!
正弦定理と余弦定理のどちらも利用する問題なので、『図形と計量』の復習にはもってこいの問題です!
問題
正弦定理 $\displaystyle\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$ より
$a:b:c=\sin A:\sin B:\sin C=3:5:7$
$a=3k$,$b=5k$,$c=7k$ ($k>0$) とおける
最も長い辺が $\textrm{AB}$ であるから、その対角 $C$ が最も大きい角である
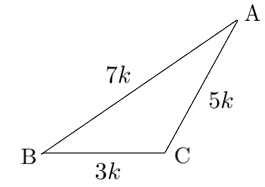
$0^\circ<C<180^\circ$ より $C=120^\circ$
正弦(sin)の比と辺の長さの比
正弦定理 $\displaystyle{\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R}$ より
$\displaystyle{\sin A=\frac{a}{2R}}$,$\displaystyle{\sin B=\frac{b}{2R}}$,$\displaystyle{\sin C=\frac{c}{2R}}$
これより
\begin{eqnarray} & & \sin A:\sin B:\sin C \\\\ &=& \frac{a}{2R}:\frac{b}{2R}:\frac{c}{2R} \\\\ &=& a:b:c \end{eqnarray}最大角と最大辺
最大角は、最大辺の対角である(最大辺は、最大角の対辺である)
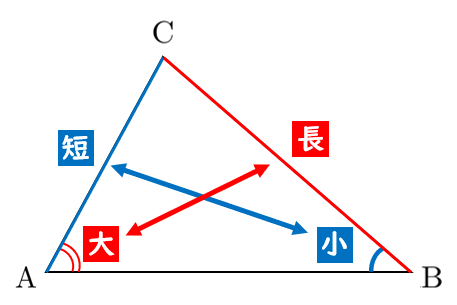
$A$$>$$B$ $\Longleftrightarrow$ $a$$>$$b$
解説
<問題を解くポイント>
① $\sin A=\sin B=\sin C=a:b:c$ を利用して、正弦(sin)の比を辺の長さの比と考える
② 最大角は、最大辺の対角を考える
③ 余弦定理を用いて、3辺から角(cos)を求める
正弦定理 $\displaystyle\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$ より
$a:b:c=\sin A:\sin B:\sin C=3:5:7$
$a=3k$,$b=5k$,$c=7k$ ($k>0$) とおける
最も長い辺が $\textrm{AB}$ であるから、その対角 $C$ が最も大きい角である

$0^\circ<C<180^\circ$ より $C=120^\circ$
減点される解答
正弦定理 $\displaystyle\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$ より
$a:b:c=\sin A:\sin B:\sin C=3:5:7$
$a=3$,$b=5$,$c=7$ で考える ←減点される
最も長い辺が $\textrm{AB}$ であるから、その対角 $C$ が最も大きい角なので
$0^\circ<C<180^\circ$ より $C=120^\circ$
「 $a:b:c=3:5:7$ から $a=3$,$b=5$,$c=7$ 」で減点されます。
$a:b:c=3:5:7$ ということは、
「$a=6$,$b=10$,$c=14$」 や「$a=9$,$b=15$,$c=21$」なども考えられます。
$a:b:c=3:5:7$ という辺の長さの比が分かっただけで、辺の長さが確定したわけではないので、「$a=3k$,$b=5k$,$c=7k$ ($k>0$) 」とする必要があります。




コメント