点と点の距離

高校数学Ⅱで学ぶ『点と点の距離』についてわかりやすく解説！

座標平面に関する問題では頻出です！

確実に使いこなせるようにマスターしましょう！

座標

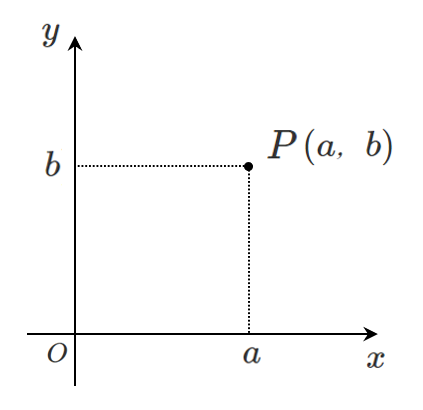
$\textrm{P}$ の座標が $(a，b)$ を　$\textrm{P}(a，b)$　とかく

三平方の定理

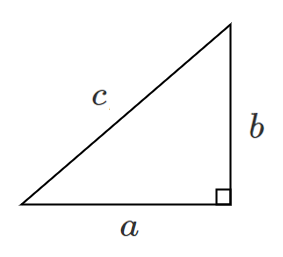
$c^2=a^2+b^2$ より，

　$c=±\sqrt{a^2+b^2}$

$c>0$ より，　$c=\sqrt{a^2+b^2}$

原点との距離

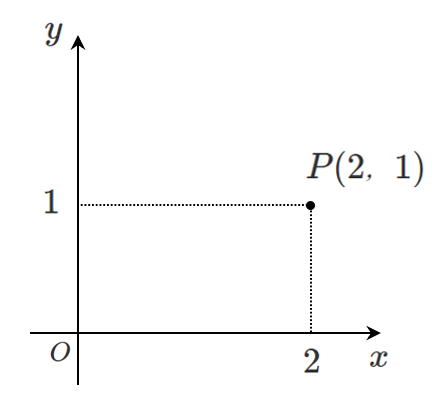
直角三角形を作る

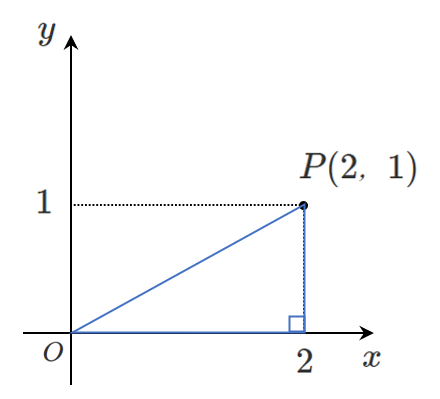
三平方の定理より，

　$\textrm{OP}=\sqrt{2^2+1^2}=\sqrt{5}$

　

点と点の距離

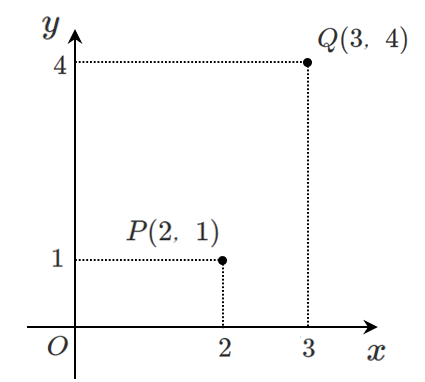
直角三角形を作る

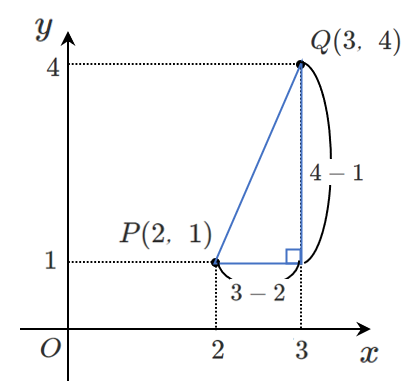
三平方の定理より，

　$\textrm{PQ}=\sqrt{(3-2)^2+(4-1)^2}=\sqrt{10}$

簡単に表すと

　点 $(○，□)$ と点 $(●，■)$ の距離は　$\sqrt{(●-○)^2+(■-□)^2}$

$2$ 乗されるので，$●-○$ でも $○-●$ でもよい

まとめ

● 三平方の定理

　斜辺を $c$，他の辺を $a$，$b$ とするとき

　　$c^2=a^2+b^2$　すなわち　$c=\sqrt{a^2+b^2}$

● 原点との距離

　　原点と点 $(a，b)$ の距離は　$\sqrt{a^2+b^2}$

● 点と点の距離

　　点 $(a，b)$ と点 $(c，d)$ の距離は　$\sqrt{(c-a)^2+(d-b)^2}$

　　点 $(○，□)$ と点 $(●，■)$ の距離は　$\sqrt{(●-○)^2+(■-□)^2}$

問題