高校数学Ⅱで学ぶ『点と直線の距離』について解説!
図形と方程式の単元で最も使う公式と言っても過言ではない公式です!
この投稿を見れば、『点と直線の距離』はバッチリ!

「図形と方程式」の中では最重要といっても過言ではない「点と直線の距離」をマスターしよう!
点と直線の距離とは
点から直線に下ろした垂線の長さが「点と直線の距離」
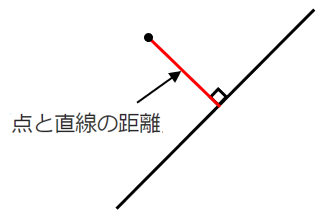
点と直線の距離は $d$ という文字がよく使われる
「distance(距離)」の頭文字と覚えておこう

点と直線の最短距離を結んだ線分の長さだね!
原点と直線の距離を求める

公式なしで「原点と直線の距離」を求めてみよう!
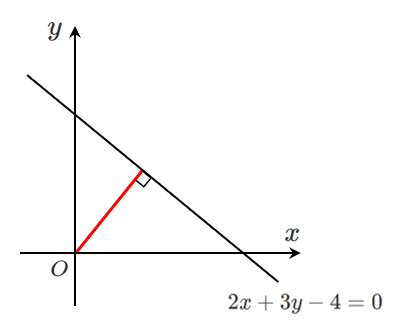
$2x+3y-4=0$ を式変形すると $\displaystyle{y=-\frac{2}{3}x+\frac{4}{3}}$
直線 $\displaystyle{y=-\frac{2}{3}x+\frac{4}{3}}$ と垂直で原点を通る直線は $\displaystyle{y=\frac{3}{2}x}$
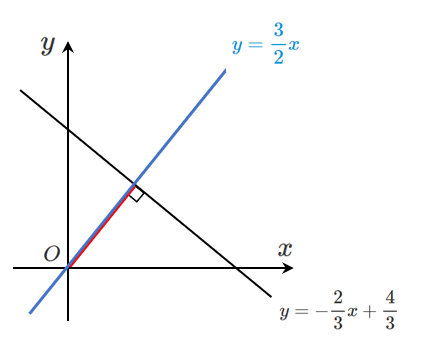
$\displaystyle{y=-\frac{2}{3}x+\frac{4}{3}}$ と $\displaystyle{y=\frac{3}{2}x}$ の交点を求めると
(連立方程式を解くと求まる)
$\displaystyle{\left(\frac{8}{13},\frac{12}{13}\right)}$
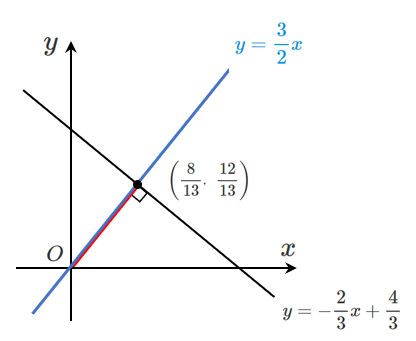
原点と直線 $2x+3y-4=0$ の距離 $d$ は
原点と点 $\displaystyle{\left(\frac{8}{13},\frac{12}{13}\right)}$ の距離と等しいので
$\displaystyle{d=\sqrt{\left(\frac{8}{13}\right)^2+\left(\frac{12}{13}\right)^2}}$
$\displaystyle{=\sqrt{\left(\frac{4\cdot2}{13}\right)^2+\left(\frac{4\cdot3}{13}\right)^2}}$
$\displaystyle{=\sqrt{\frac{4^2\cdot2^2+4^2\cdot3^2}{13^2}}}$
$\displaystyle{=\sqrt{\frac{4^2(2^2+3^2)}{13^2}}}$
$\displaystyle{=\sqrt{\frac{4^2\cdot13}{13^2}}}$
$\displaystyle{=\frac{4}{\sqrt{13}}}$

公式がなくても「点と直線の距離」を求めることができるけど,結構計算が大変なので公式を求めてみよう!
原点と直線の距離の公式
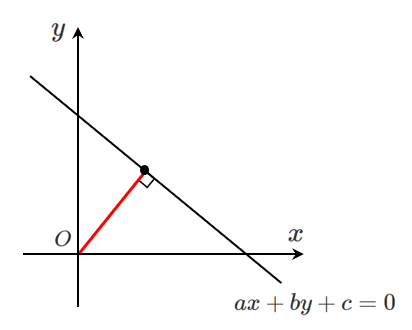
$ax+by+c=0$ を式変形すると $\displaystyle{y=-\frac{a}{b}x-\frac{c}{b}}$
直線 $\displaystyle{y=-\frac{a}{b}x-\frac{c}{b}}$ と垂直で原点を通る直線は $\displaystyle{y=\frac{b}{a}x}$
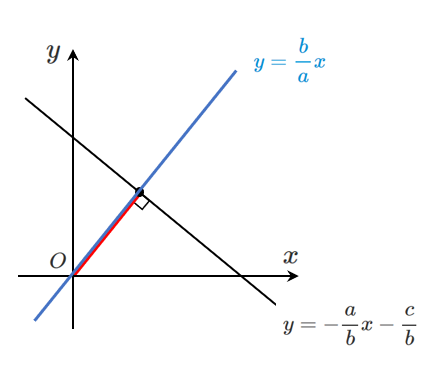
$\displaystyle{y=-\frac{a}{b}x-\frac{c}{b}}$ と $\displaystyle{y=\frac{b}{a}x}$ の交点を求めると
$y$ を消去して $\displaystyle{\frac{b}{a}x=-\frac{a}{b}x-\frac{c}{b}}$
$\displaystyle{\frac{b}{a}x+\frac{a}{b}x=-\frac{c}{b}}$
$\displaystyle{\frac{b^2}{ab}x+\frac{a^2}{ab}x=-\frac{c}{b}}$
$\displaystyle{\frac{a^2+b^2}{ab}x=-\frac{c}{b}}$
$\displaystyle{x=-\frac{ac}{a^2+b^2}}$
これを $\displaystyle{y=\frac{b}{a}x}$ に代入すると
$\displaystyle{y=-\frac{bc}{a^2+b^2}x}$
以上より,$\displaystyle{y=-\frac{a}{b}x-\frac{c}{b}}$ と $\displaystyle{y=\frac{b}{a}x}$ の交点は
$\displaystyle{\left(-\frac{ac}{a^2+b^2},-\frac{bc}{a^2+b^2}\right)}$
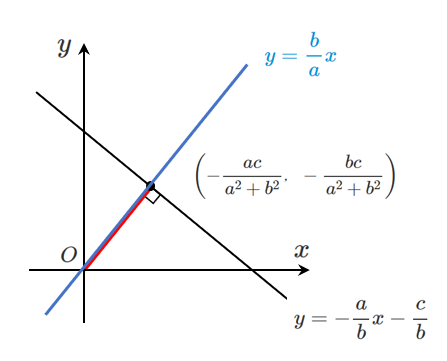
原点と直線 $ax+by+c=0$ の距離 $d$ は
原点と点 $\displaystyle{\left(-\frac{ac}{a^2+b^2},-\frac{bc}{a^2+b^2}\right)}$ の距離と等しいので
$\displaystyle{d=\sqrt{\left(-\frac{ac}{a^2+b^2}\right)^2+\left(-\frac{bc}{a^2+b^2}\right)^2}}$
$\displaystyle{=\sqrt{\frac{a^2c^2+b^2c^2}{(a^2+b^2)^2}}}$
$\displaystyle{=\sqrt{\frac{c^2(a^2+b^2)}{(a^2+b^2)^2}}}$
$\displaystyle{=\sqrt{\frac{c^2}{a^2+b^2}}}$
$\displaystyle{=\frac{|c|}{\sqrt{a^2+b^2}}}$ ( $\sqrt{c^2}=|c|$ を用いている)

計算は大変だったけど,「原点と直線の距離」の公式が求まったよ!
点と直線の距離の公式

上の公式は原点しか使えないので,ちょっと不便な公式だよ!
どこの点でも直線との距離が求まる「点と直線の距離」公式を求めよう!
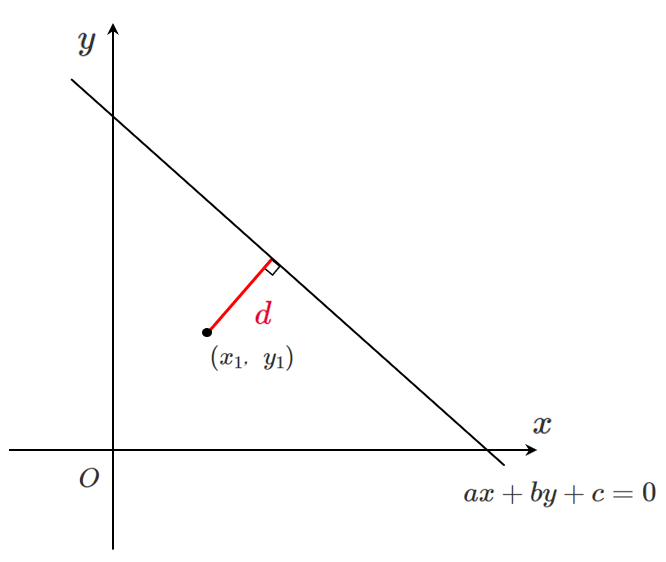

どうやって考える?

「原点と直線の距離」は公式を求めたから使いたいところだね!

素晴らしい発想だね!
どうやったら「原点と直線の距離」公式を使えるかな?

点 $(x_1,y_1)$ を原点に平行移動して,直線も同様に平行移動したら使えそうだよ!
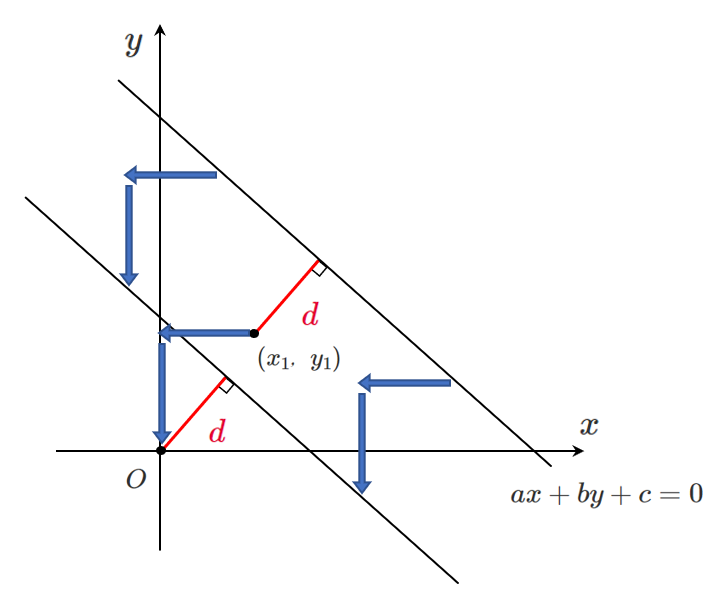

その通り!
原点と平行移動した直線の距離を「原点と直線の距離」公式で求めたらいいね!
点 $(x_1,y_1)$ を原点に平行移動するには
$x$ 軸方向に $-x_1$,$y$ 軸方向に $-y_1$ だけ平行移動すればよい
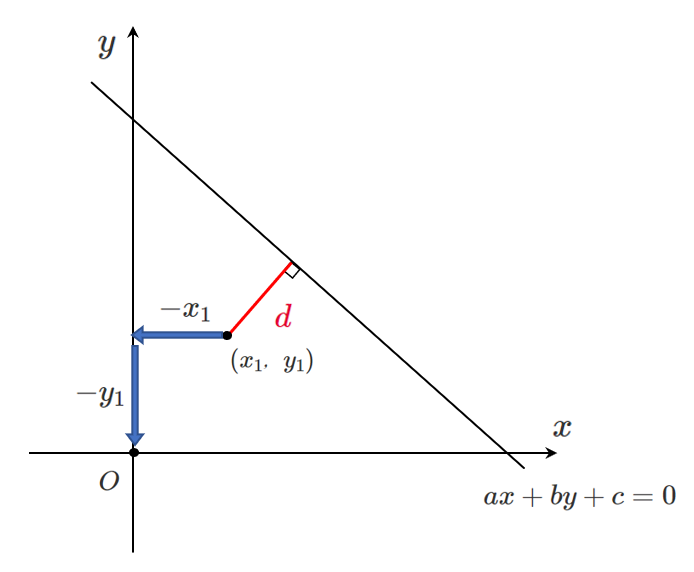
同様に,直線 $ax+by+c=0$ を
$x$ 軸方向に $-x_1$,$y$ 軸方向に $-y_1$ だけ平行移動すると
$a(x+x_1)+b(y+y_1)+c=0$
$ax+by+ax_1+by_1+c=0$
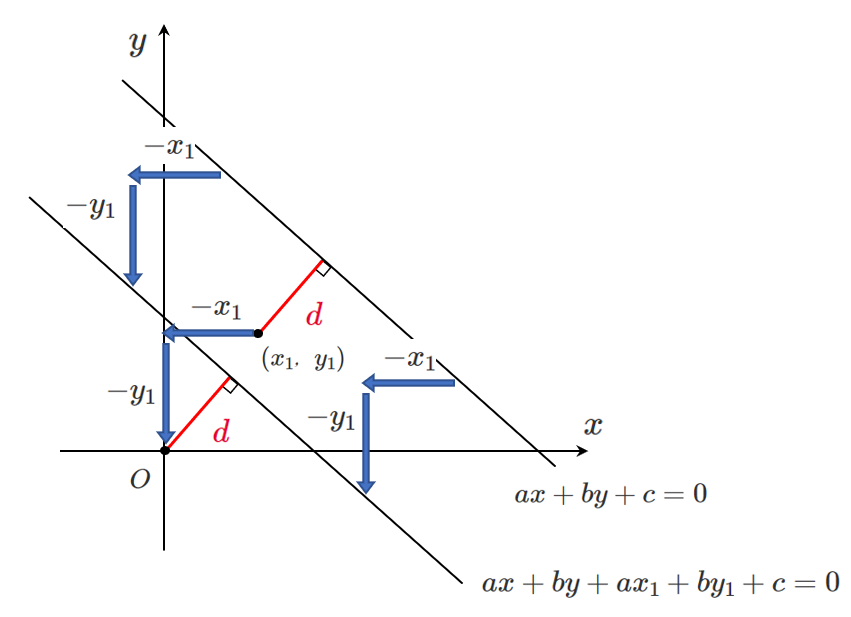
原点と直線 $ax+by+$$ax_1+by_1+c$$=0$ の距離が $d$ と等しいので
「原点と直線の距離」公式
原点と直線 $○x+□y+$$△$$=0$ の距離は $\displaystyle{\frac{|△|}{\sqrt{○^2+□^2}}}$
を用いて
$\displaystyle{d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}}$

考え方をきちんと理解しておこう!
点 $(x_1,y_1)$ と直線 $ax+by+c=0$ の距離 $d$ は
$\displaystyle{d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}}$
原点と直線の距離の公式は覚えなくてよい
点 $(x_1,y_1)$ と直線 $ax+by+c=0$ の距離 $d$ は
$\displaystyle{d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}}$
を覚えておけば
原点は $x_1=0$,$y_1=0$ となるので
原点と直線 $ax+by+c=0$ の距離は $\displaystyle{d=\frac{|c|}{\sqrt{a^2+b^2}}}$
と求めることができる

覚える公式はなるべく減らしておきたいね!
点と直線の距離の公式を使う
(1) 原点と直線 $x-3y-1=0$
(2) 点 $(2,1)$ と直線 $3x+4y+5=0$
(1) 原点と直線 $x+3y-1=0$
$\displaystyle{d=\frac{|1\cdot0-3\cdot0-1|}{\sqrt{1^2+(-3)^2}}}$
$\displaystyle{=\frac{|-1|}{\sqrt{10}}}$
$\displaystyle{=\frac{1}{\sqrt{10}}}$
(2) 点 $(2,1)$ と直線 $3x+4y+5=0$
$\displaystyle{d=\frac{|3\cdot2+4\cdot1+5|}{\sqrt{3^2+4^2}}}$
$\displaystyle{=\frac{|15|}{\sqrt{25}}}$
$\displaystyle{=\frac{15}{5}}$
$=3$

ルートと絶対値の計算を間違えないように気を付けよう!
まとめ
● 点と直線の距離とは
点から直線に垂線を下ろしたときの垂線の長さ
● 点と直線の距離
点 $(x_1,y_1)$ と直線 $ax+by+c=0$ の距離 $d$ は
$\displaystyle{d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}}$

覚えにくい公式だけど,「図形と方程式」の中では一番覚えておかないといけない公式!
多くの問題で使用するので,覚えて使えるようにしておこう!




コメント