『絶対不等式』とは、どのような値をとっても成り立つ不等式のことをいいます。
この絶対不等式を利用した次のような問いがよく出題されます。
解がすべての実数であるような定数 $k$ の値の範囲を求めよ。
すべての実数 $x$ について成り立つような定数 $k$ の範囲を求めよ。
問題文だけ見ると少し難しそうなので、『絶対不等式』は苦手な人が多い問題の1つです。
『絶対不等式』を解くコツは、2次不等式を解くときと同様に、2次関数のグラフを利用することです。
この投稿を見れば、『絶対不等式』を解けるようになります。
問題
(2) $k≠2$ とする。2次不等式 $(k-2)x^2+2(k-1)x+3k-5<0$ の解がすべての実数であるとき,定数 $k$ の値の範囲を求めよ。
(1) $y=x^2+2kx-3k+4$ とおくと
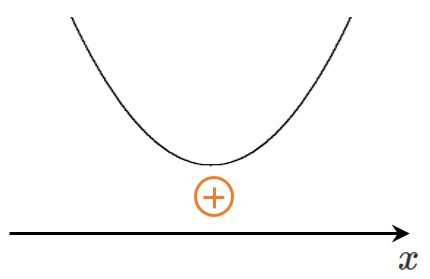
グラフが $x$ 軸より上側にあるとき
解がすべての実数となる
$x^2+2kx-3k+4=0$ の判別式を $D$ とすると
グラフが $x$ 軸と交わらないので $D<0$
$\displaystyle{\frac{D}{4}=k^2-(-3k+4)=(k-1)(k+4)}$
$D<0$ より $-4<k<1$
(2) $y=(k-2)x^2+2(k-1)x+3k-5$ とおくと
グラフが 上に凸 かつ $x$ 軸より上側にある とき
解がすべての実数となる
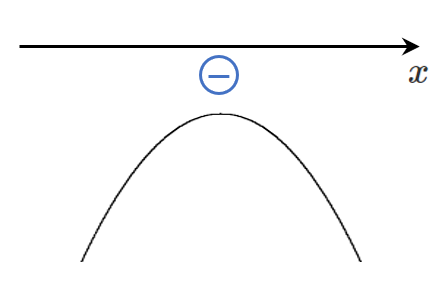
下に凸なので $k-2<0$ すなわち $k<2$ … ①
$(k-2)x^2+2(k-1)x+3k-5=0$ の判別式を $D$ とすると
グラフが $x$ 軸と交わらないので $D<0$
$\displaystyle{\frac{D}{4}=(k-1)^2-(k-2)(3k-5)=-2k^2+9k-9=-(2k-3)(k-3)}$
$D<0$ より $-(2k-3)(k-3)<0$ すなわち $(2k-3)(k-3)>0$
これを解いて $\displaystyle{\frac{3}{2}<k<3}$ … ②
①,②の共通範囲をとって $\displaystyle{\frac{3}{2}<k<2}$
絶対不等式のポイント
グラフの形(下に凸か上に凸か)とグラフと $x$ 軸の共有点の個数を考える
●2次不等式 $ax^2+bx+c>0$ の解がすべての実数
(すべての実数 $x$ について $ax^2+bx+c>0$ が成り立つ)
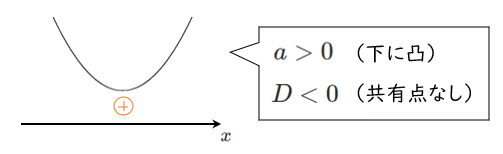
●2次不等式 $ax^2+bx+c<0$ の解がすべての実数
(すべての実数 $x$ について $ax^2+bx+c<0$ が成り立つ)
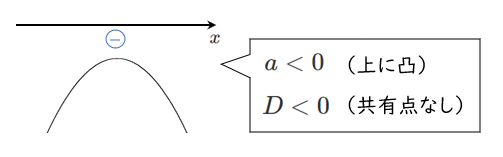
絶対不等式(グラフの形が決まっている)
●2次不等式 $ax^2+bx+c>0$ の解がすべての実数
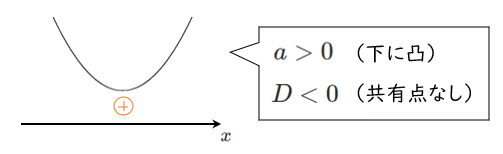
グラフの形は下に凸で定まっているので、$D<0$ のみ考える
(1) $y=x^2+2kx-3k+4$ とおくと
グラフが $x$ 軸より上側にあるとき
解がすべての実数となる
$x^2+2kx-3k+4=0$ の判別式を $D$ とすると
グラフが $x$ 軸と交わらないので $D<0$
$\displaystyle{\frac{D}{4}=k^2-(-3k+4)=(k-1)(k+4)}$

絶対不等式(グラフの形が決まっていない)
●2次不等式 $ax^2+bx+c<0$ の解がすべての実数
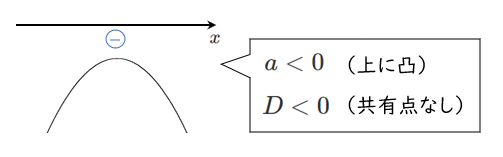
(2) $y=(k-2)x^2+2(k-1)x+3k-5$ とおくと
グラフが 上に凸 かつ $x$ 軸より上側にある とき
解がすべての実数となる

下に凸なので $k-2<0$ すなわち $k<2$ … ①
$(k-2)x^2+2(k-1)x+3k-5=0$ の判別式を $D$ とすると
グラフが $x$ 軸と交わらないので $D<0$
$\displaystyle{\frac{D}{4}=(k-1)^2-(k-2)(3k-5)=-2k^2+9k-9=-(2k-3)(k-3)}$
$D<0$ より $-(2k-3)(k-3)<0$ すなわち $(2k-3)(k-3)>0$
これを解いて $\displaystyle{\frac{3}{2}<k<3}$ … ②
①,②の共通範囲をとって $\displaystyle{\frac{3}{2}<k<2}$
🔵2次関数のグラフの平行移動・対称移動
🔴軸に定数を含む2次関数の最大・最小の場合分け
🔴定義域の片端に定数を含む2次関数の最大・最小の場合分け
🔴定義域の両端に定数を含む2次関数の最大・最小の場合分け
🔵因数分解形の利用した2次関数の決定
🔴場合分けが必要な文字係数の方程式
🔵2次関数がx軸から切り取る線分の長さ
🔴文字係数の2次不等式
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント