高校数学Ⅱで学ぶ『複素数の範囲での2次式の因数分解』についてわかりやすく解説しました!
中学や高校数学Ⅰで習った2次式の因数分解は『整数の範囲での因数分解』だったので、因数分解できない式も登場しました!
因数分解を複素数の範囲まで広げると、係数が実数である2次式は常に1次式の積に因数分解できます!
この投稿を見れば、『複素数の範囲での2次式の因数分解』はバッチリです!
2次式の因数分解
2次式の因数分解
2次方程式 $ax^2+bx+c=0$ ($a≠0$) の解を $\alpha$,$\beta$ とすると
$ax^2+bx+c=a(x-\alpha)(x-\beta)$ と因数分解できる
$ax^2+bx+c=a(x-\alpha)(x-\beta)$ と因数分解できる
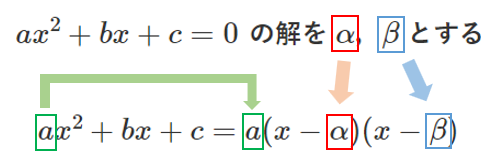
解と係数の関係を用いて説明
2次方程式 $ax^2+bx+c=0$ ($a≠0$) の解を $\alpha$,$\beta$ とすると
\begin{eqnarray} ax^2+bx+c &=& a\left(x^2+\frac{b}{a}x+\frac{c}{a}\right) \\ &=& a\{x^2-(\alpha+\beta)x+\alpha\beta\} \\ &=& a(x-\alpha)(x-\beta) \end{eqnarray}【補足】解と係数の関係 $\displaystyle{\alpha+\beta=-\frac{b}{a}}$,$\displaystyle{\alpha\beta=\frac{c}{a}}$
実数係数の2次式は、複素数の範囲で常に1次式の積に因数分解できる。
問題
問題
次の2次式を,複素数の範囲で因数分解せよ。
(1) $2x^2-2x-1$ (2) $x^2-2x+4$
(1) $2x^2-2x-1$ (2) $x^2-2x+4$
解答
(1) 2次方程式 $2x^2-2x-1=0$ の解は $\displaystyle{x=\frac{1\pm\sqrt{3}}{2}}$
よって $\displaystyle{2x^2-2x-1=2\left(x-\frac{1+\sqrt{3}}{2}\right)\left(x-\frac{1-\sqrt{3}}{2}\right)}$

(2) 2次方程式 $x^2-2x+4=0$ の解は $x=1\pm\sqrt{3}i$ より
よって $x^2-2x+4=\{x-(1+\sqrt{3}i)\}\{x-(1-\sqrt{3}i)\}$
$=(x-1-\sqrt{3}i)(x-1+\sqrt{3}i)$





コメント