
連立不等式を満たす領域を図示しよう!
連立とは

連立方程式から「連立」について考えてみよう!
$
\left\{\begin{align}
&x+2y=1 \cdots ①\\
&2x+y=5 \cdots ②
\end{align}\right.
$
$①×2-②$より $y=-1$
①に代入して $x=3$
したがって,連立方程式の解は $(x,y)=(3,-1)$

$(x,y)=(3,-1)$ は①と②を同時に満たす $x$ と $y$ の組合せのこと!
「連立方程式を解く」とは「それらの式を同時に満たす文字の値を求めること」!

「連立」は「同時に満たすものを求める」!
連立不等式を満たす領域(直線と直線)
不等式 $y < x+1$ を満たす領域は
直線 $y=x+1$ の下側
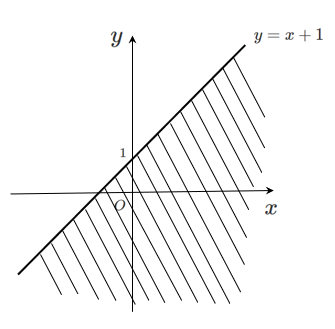
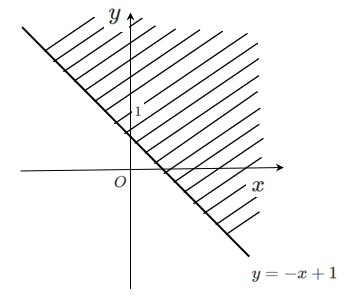
不等式 $y > -x+1$ を満たす領域は
直線 $y=-x+1$ の上側
連立不等式を図示することは,
これらを同時に満たす領域を図示することなので,
連立不等式を満たす領域は
直線 $y=x+1$ の下側 かつ 直線 $y=-x+1$ の上側
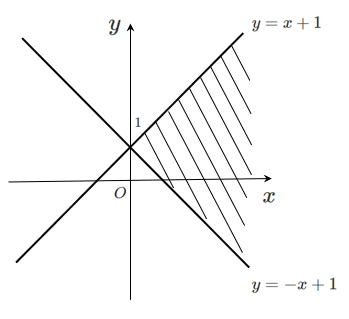

それぞれの不等式の領域の共通部分を図示すればいいね!
連立不等式を満たす領域(直線と円)
不等式 $y < x+1$ を満たす領域は
直線 $y=x+1$ の下側

不等式 $x^2+y^2 < 4$ を満たす領域は
円 $x^2+y^2=4$ の内側
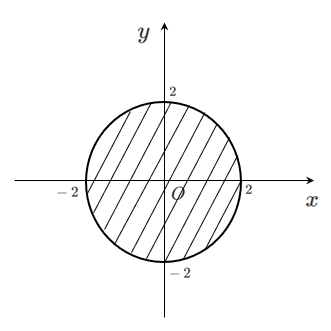
連立不等式を図示することは,
これらを同時に満たす領域を図示することなので,
連立不等式を満たす領域は
直線 $y=x+1$ の下側 かつ 円 $x^2+y^2=4$ の内側
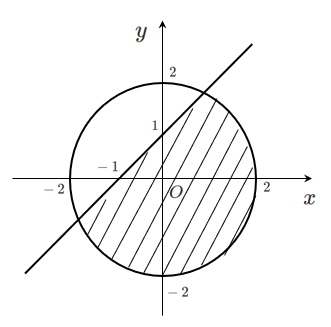

直線の上下と円の内外をはっきりさせれば,共通部分で簡単に図示できるね!
まとめ
● 連立不等式を満たす領域
連立不等式を満たす領域は,それぞれの不等式の領域の共通部分をとる
問題
次の連立不等式を満たす領域を図示せよ。
(1) $ \left\{\begin{align} &y > x+1 \\ &y > -x+1 \end{align}\right. $
(2) $ \left\{\begin{align} &y > x+1 \\ &x^2+y^2 > 4 \end{align}\right. $
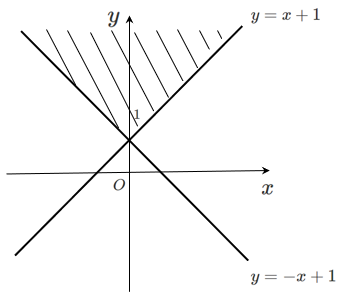
(1) $
\left\{\begin{align}
&y > x+1 \\
&y > -x+1
\end{align}\right.
$
直線 $y=x+1$ の上側 かつ 直線 $y=-x+1$ の上側
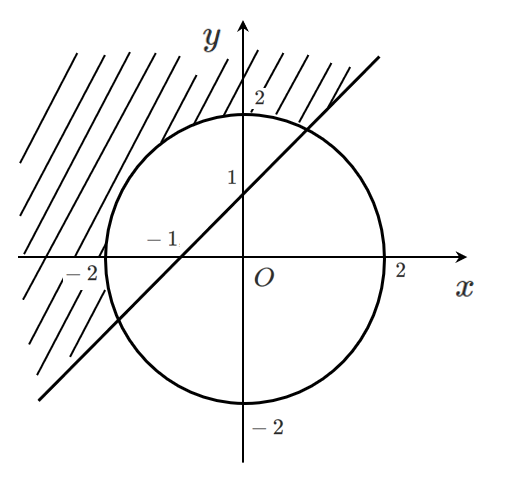
(2) $
\left\{\begin{align}
&y > x+1 \\
&x^2+y^2 > 4
\end{align}\right.
$
直線 $y=x+1$ の上側 かつ 円 $x^2+y^2=4$ の外側

これで,領域の図示の基本は完璧!




コメント