連立不等式は計算の基本!
数学が苦手な人でも必ずわかるように説明します!
解法をきちんと理解して,ミスなく確実に計算できるように練習しましょう!

今回解説する問題はこれ!
問題
(1) 次の連立不等式を解け。
\begin{align}
\left\{
\begin{array}{ll}
x-1≦5-2x \\
3x+1>2x-1
\end{array}
\right.
\end{align}
(2) 不等式 $3x-7 < x-1 ≦ -x+3$ を解け。
(3) 不等式 $3 < 2x-1 < 7$ を解け。
(3) 不等式 $3 < 2x-1 < 7$ を解け。
連立不等式とは
連立不等式とは2つ以上の不等式を組み合わせたものをいい,それらの不等式をすべて満たす値の範囲を連立不等式の解という
\begin{align} \left\{ \begin{array}{ll} x-1≦5-2x \\ 3x+1>2x-1 \end{array} \right. \end{align}
連立方程式と似ているね!

問題は似ているけど,不等式だから少し難しいよ!
解法をきちんと確認しておこう!
連立不等式の解法
連立不等式の解き方
- それぞれの不等式を解く
- 共通範囲を取る
問題1
次の連立不等式を解け。
\begin{align}
\left\{
\begin{array}{ll}
x-1≦5-2x \\
3x+1>2x-1
\end{array}
\right.
\end{align}
解答
\begin{align}
\left\{
\begin{array}{ll}
x-1≦5-2x \cdots ①\\
3x+1>2x-1 \cdots ②
\end{array}
\right.
\end{align}
①より
\begin{eqnarray} x-1 & ≦ & 5-2x \\ 3x & ≦ & 6 \\ x & ≦ & 2 \end{eqnarray}②より
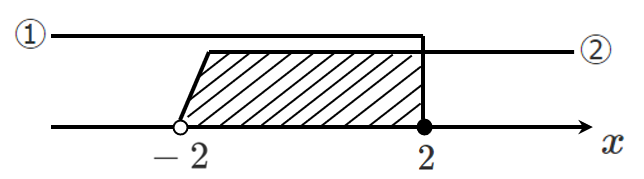
\begin{eqnarray} 3x+1 & > & 2x-1 \\ x & > & -2 \end{eqnarray}①と②の共通範囲をとって

$-2 < x ≦ 2$
A<B<C の解法
$A < B < C$ の解法
$A < B < C$ を以下の連立不等式にして解く
\begin{align}
\left\{
\begin{array}{ll}
A < B \\
B < C
\end{array}
\right.
\end{align}
問題2
不等式 $3x-7 < x-1 ≦ -x+3$ を解け。
解答
$3x-7 < x-1 ≦ -x+3$ は以下の連立不等式で解ける
\begin{align} \left\{ \begin{array}{ll} 3x-7 < x-1 \cdots ①\\ x-1 ≦ -x+3 \cdots ② \end{array} \right. \end{align}①より
\begin{eqnarray} 3x-7 & < & x-1 \\ 2x & < & 6 \\ x & < & 3 \end{eqnarray}②より
\begin{eqnarray} x-1 & ≦ & -x+3 \\ 2x & ≦ & 4 \\ x & ≦ & 2 \end{eqnarray}①と②の共通範囲をとって
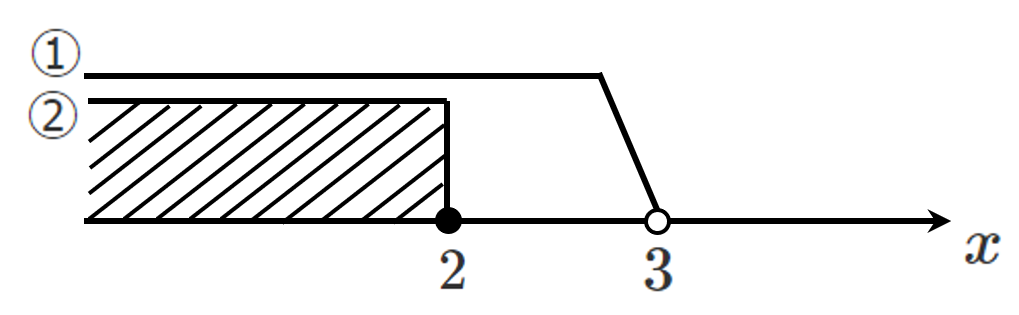
$x ≦ 2$
問題3
不等式 $3 < 2x-1 < 7$ を解け。

\begin{align}
\left\{
\begin{array}{ll}
3 < 2x-1 \cdots ①\\
2x-1 ≦ 7 \cdots ②
\end{array}
\right.
\end{align}
で解けばいいのかな?

真ん中しか $x$ がない場合は,以下のように解けるよ!
解答
$3 < 2x-1 < 7$
⇩$1$ を足す
$4 < 2x< 8$
⇩$2$ で割る
$2 < x < 4$(答)
あなたのオススメ
🔴文字係数の1次不等式を場合分けして解く方法を解説
🔴1次不等式の整数解の個数に関する問題を解説
🔰絶対値のはずし方をわかりやすく解説
🔰絶対値の方程式と不等式の基本を解説
🔰絶対値の方程式と不等式をわかりやすく解説
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント