集合
集合…範囲がはっきりしたものの集まり
要素…集合を構成しているひとつひとつ
例 $5$ 以下の自然数全体の集合 $A$
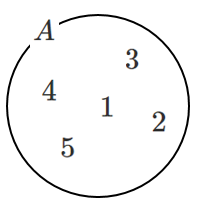
$A$ の要素は $1,2,3,4,5$
集合 $A$ を以下のように表す
$A=\{1,2,3,4,5\}$
$\{ \}$ の中に要素を書くと、その要素が集まった集合を表す
共通部分
\(A \cap B\) ($A$ かつ $B$)… $A$ と$B$ の共通部分
$A$ と $B$ の両方に属する集合
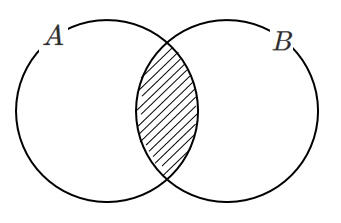
和集合
\(A \cup B\)($A$ または $B$)… $A$ と $B$ の和集合
$A$ と $B$ の少なくとも一方に属する集合
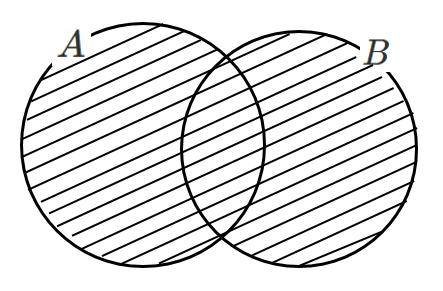
補集合
\(\overline{A}\) … 集合 $A$ の補集合
$U$ は全体集合
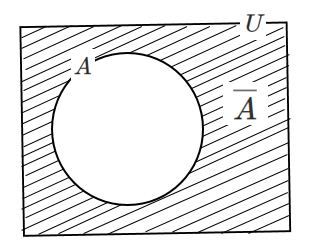
詳しい解説はこれ↓
集合の要素の個数の表し方
$n(A)$ … 集合 $A$ の要素の個数
例 $5$ 以下の自然数全体の集合 $A$

$n(A)=5$(集合 $A$ の個数は $5$ 個)

$n( )$ の $n$ は「個数」という意味の「number」の頭文字と覚えておこう!
和集合の要素の個数
和集合 $A \cup B$ の要素の個数は以下のように表せる

$n(A)=a$,$n(B)=b$,$n(A \cap B)=c$ とすると
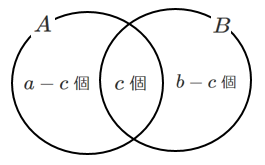
$n(A \cup B)=(a-c)+(b-c)+c$
$=a+b-c$
$=n(A)+n(B)-n(A \cap B)$

$n(A)+n(B)$ だと共通部分である $n(A \cap B)$ を2回足していることになるから,$n(A \cap B)$ を引くんだね!
補集合の要素の個数
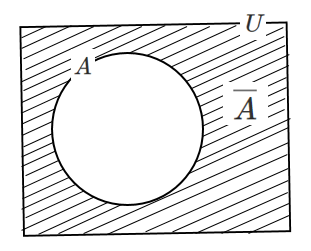
全体集合 $U$ の要素の個数から集合 $A$ の要素の個数を引く
まとめ
● 集合
\(A \cap B\) ($A$ かつ $B$)… $A$ と$B$ の共通部分
\(A \cup B\)($A$ または $B$)… $A$ と $B$ の和集合
\(\overline{A}\) … 集合 $A$ の補集合
● 要素の個数
$n(A)$ … 集合 $A$ の要素の個数
● 和集合 \(A \cap B\) の要素の個数
$n(A \cup B)=n(A)+n(B)-n(A \cap B)$
● 補集合の要素の個数
$n(\overline{A})=n(U)-n(A)$
問題
$n(U)=50$,$n(A)=30$,$n(B)=25$,$n(A \cap B)=15$
であるとき,次の要素の個数を求めよ。
(1) $A \cup B$
(2) $\overline{A}$
(3) $A \cap \overline{B}$
(4) $\overline{A \cup B}$
(5) $\overline{A} \cap \overline{B}$
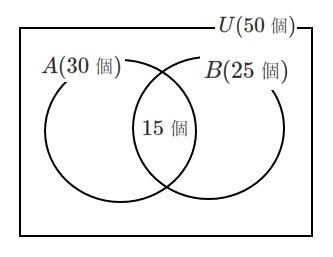
(1) $A \cup B$
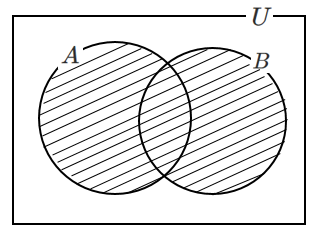
$n(A \cup B)=n(A)+n(B)-n(A \cap B)$
$=30+25-15$
$=40$
(2) $\overline{A}$
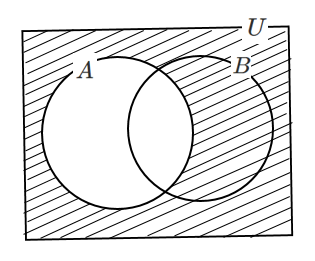
$n(\overline{A})=n(U)-n(A)$
$=50-30$
$=20$
(3) $A \cap \overline{B}$($A$ の中 かつ $B$ の外)
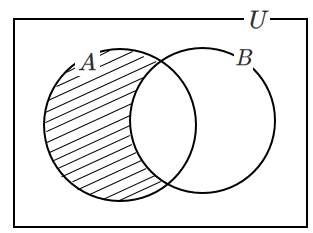
$n(A \cap \overline{B})=n(A)-n(A \cap B)$
$=30-15$
$=15$
(4) $\overline{A \cup B}$
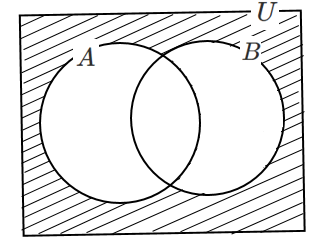
$n(\overline{A \cup B})=n(U)-n(A \cup B)$
$=50-40$
$=10$
(5) $\overline{A} \cap \overline{B}$
ド・モルガンの法則より
$\overline{A} \cap \overline{B}=\overline{A \cup B}$
よって $n(\overline{A} \cap \overline{B})=n(\overline{A \cup B})=10$
ド・モルガンの法則はこれ↓


図を描いてみることが大切!
ド・モルガンの法則も使えるように!




コメント