高校数学Ⅱの【図形と方程式】で学ぶ『領域における最大・最小』について解説!
領域の応用問題で,定期考査では必ず問われる重要問題です!
理解して解けるように練習しましょう!
この投稿を見れば,領域における最大・最小に関する問題はバッチリ!
解説する問題はこれです↓
解法の手順
手順1 与えられた不等式を満たす領域 $D$ を図示する
手順2 与えられた $1$ 次式 $x+y$ を $k$ とおく($x+y=k$ … ①)
➡ $x+y$ の最大値・最小値は,$k$ の最大値・最小値と等しい
手順3 式変形すると $y=-x+k$
➡ 傾き $-1$,$y$ 切片 $k$ の直線である
手順4 領域 $D$ と共有点をもつように直線①を平行移動させて,
$y$ 切片 $k$ が最大値・最小値をとるときを考える
【補足】
例えば,「$2x+x$ の最大値・最小値」も同様に,$2x+y=k$ とおいて $y$ 切片に着目する
問題
2直線 $2x+y=5$,$x+2y=4$ の交点の座標は $(2,1)$
連立不等式の表す領域を $D$ とすると,
$D$ は右の図の斜線部分であり,境界線を含む
$x+y=k$ … ① とおくと,$y=-x+k$ より,
①は傾き $-1$,$y$ 切片 $k$ の直線を表す
よって,求める最大値および最小値は,
直線①が領域 $D$ と共有点をもつときの
$y$ 切片 $k$ の最大値および最小値である
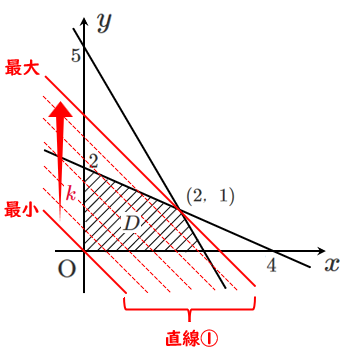
上図のように,
直線①を平行移動させて考える
直線①が $(2,1)$ を通るとき $y$ 切片 $k$ は最大となるから,
$k=x+y$ より,$k$ は $x=2$,$y=1$ のとき,最大値 $3$
直線①が 原点 を通るとき $y$ 切片 $k$ は最小となるから,
$k=x+y$ より,$k$ は $x=0$,$y=0$ のとき,最小値 $0$
したがって,$x+y$ は
$x=2$,$y=1$ のとき,最大値 $3$
$x=0$,$y=0$ のとき,最小値 $0$




コメント