高校数学Ⅱの【図形と方程式】で学ぶ『領域における最大・最小|x²+y² 』について解説!
領域の応用問題の中でも,難易度の高い問題ですが,
理解して解けるように練習して,周りと差をつけよう!
この投稿を見れば,『領域における最大・最小|x²+y² 』に関する問題はバッチリ!
解説する問題はこれです↓
解法の手順
手順1 与えられた不等式を満たす領域 $D$ を図示する
手順2 与えられた $2$ 次式 $x^2+y^2$ を $k$ とおく($x^2+y^2=k$ … ①)
➡ $x^2+y^2$ の最大値・最小値は,$k$ の最大値・最小値と等しい
➡ 中心 $(0,0)$,半径 $\sqrt{k}$ の円
手順3 領域 $D$ と共有点をもつように円①の半径を変化させて,
半径が最大値・最小値になるときを考える
問題
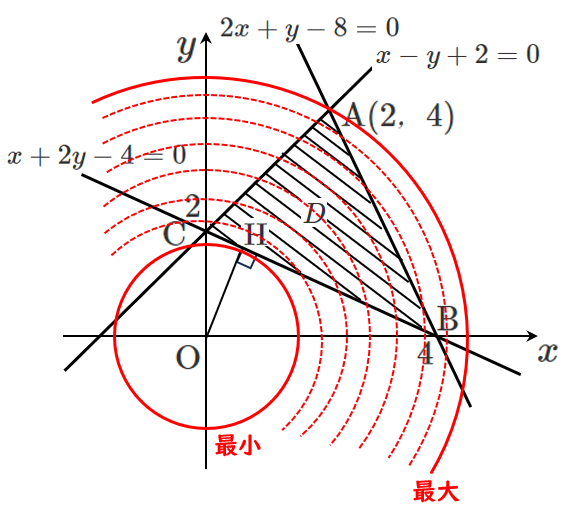
3直線 $x-y+2=0$,$2x+y-8=0$,$x+2y-4=0$ の交点を $\textrm{A}(2,4)$,$\textrm{B}(4,0)$,$\textrm{C}(0,2)$ とする
連立不等式の表す領域を $D$ とすると,
$D$ は右図の斜線部であり,境界線を含む
$x^2+y^2=k$ … ① とおくと,
①は原点を中心とする半径 $\textrm{k}$ の円を表す
求める最大値,最小値は円①が領域 $D$ と共有点をもつときの
$k$ の最大値,最小値である
(i) $k$ が最大となるのは,円①が点 $\textrm{A}(2,4)$ を通るとき
$k$ の最大値は $k=2^2+4^2=20$
(ii) $k$ が最小となるのは,円①が直線 $\textrm{BC}$ に接するとき
接点を $\textrm{H}$ とすると $\displaystyle{\textrm{OH}=\frac{|-4|}{\sqrt{1^2+2^2}}=\frac{4}{\sqrt{5}}}$
(↑点と直線の距離)
$\textrm{OH}$ と円の半径が等しいので,
$k$ の最小値は $\displaystyle{\sqrt{k}=\frac{4}{\sqrt{5}}}$ より $\displaystyle{k=\frac{16}{5}}$
直線 $\textrm{BC}$ と直線 $\textrm{OH}$ は垂直なので
直線 $\textrm{BC}$ の傾き $\displaystyle{-\frac{1}{2}}$ より,直線 $\textrm{OH}$ の傾きは $2$ である
以上より,直線 $\textrm{OH}$ の方程式は $y=2x$
直線 $\textrm{BC}$:$x+2y-4=0$ と連立すると $\displaystyle{\textrm{H}\left(\frac{4}{5},\frac{8}{5}\right)}$
(i),(ii) より,$x^2+y^2$ は
$x=2$,$y=4$ のとき 最大値 $20$
$\displaystyle{x=\frac{4}{5}}$,$\displaystyle{y=\frac{8}{5}}$ のとき 最小値 $\displaystyle{\frac{16}{5}}$




コメント