１次不等式の整数解の個数

次の連立不等式を満たす整数 $x$ がちょうど $3$ 個存在するような定数 $a$ の値の範囲を求めよ。 \begin{align} \left\{ \begin{array}{ll} 2x-5 > 3-2x　\cdots　①\\ x-a < 1　　　　\cdots　② \end{array} \right. \end{align}

　①について，

\begin{eqnarray} 2x-5 & > & 3-2x \\ 4x & > & 8 \\ x & > & 2 \\ \end{eqnarray}

　②について，

$$x<a+1$$

　①と②の共通範囲が存在するように図示すると

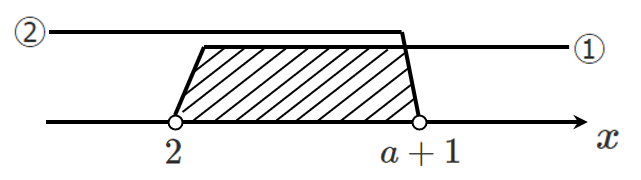
　共通範囲が存在するように図示すると，$a+1$ は $2$ よりも右側にこないといけない（$2$ よりも大きくないといけない）

　整数 $x$ がちょうど $3$ 個存在するには，以下の図のようになる

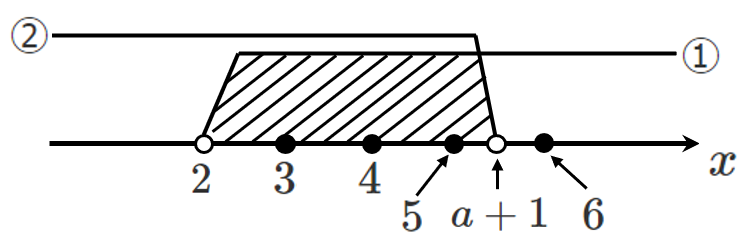
　すなわち，共通範囲には『 $3，4，5$ 』が入っている必要がある

　このような図になるためには，$a+1$ が $5$ と $6$ の間に存在しなければならないので，

$5<a+1<6$

　$5$ の方に『＝がつくかどうか』を考える
　➡ $5$ の上に $a+1$ を置いてみる

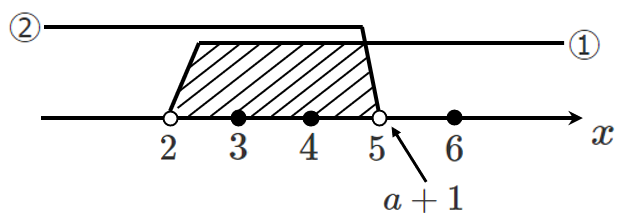
　$a+1$ の上は含まないので，$5$ は共通範囲には含まれない
　すなわち，共通範囲には『 $3，4$ 』の $2$ 個だけになるため条件を満たさない
　したがって，$5$ の方に『＝はつかない』

　

　$6$ の方に『＝がつくかどうか』を考える
　➡ $6$ の上に $a+1$ を置いてみる

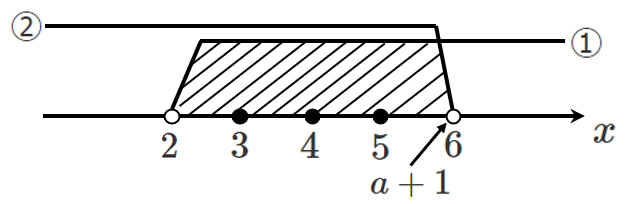
　$a+1$ の上は含まないので，$6$ は共通範囲には含まれない
　すなわち，共通範囲には『 $3，4，5$ 』の $3$ 個になるため条件を満たす
　したがって，$6$ の方に『＝はつく』

　以上より，

$5$$<$$a+1$$≦$$6$

$4<a≦5$（答）

次の連立不等式を満たす整数 $x$ がちょうど $3$ 個存在するような定数 $a$ の値の範囲を求めよ。 \begin{align} \left\{ \begin{array}{ll} 2x-5 > 3-2x　\cdots　①\\ x-a ≦ 1　　　　\cdots　② \end{array} \right. \end{align}

\begin{align} \left\{ \begin{array}{ll} x > 2　　　\cdots　①\\ x ≦ a+1　\cdots　② \end{array} \right. \end{align}

　①と②を同時に満たす整数 $x$ がちょうど $3$ 個存在するには，以下の図のようになる

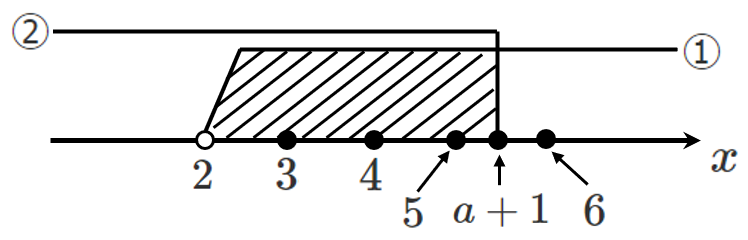
　$5$ の方に『＝がつくかどうか』を考える
　➡ $5$ の上に $a+1$ を置いてみる

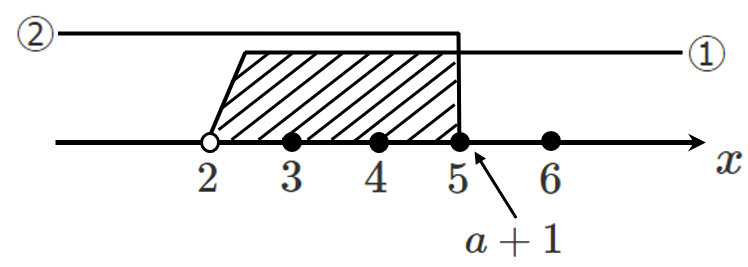
　$a+1$ の上は含むので，$5$ は共通範囲には含まれる
　すなわち，共通範囲には『 $3，4，5$ 』の $3$ 個になるため条件を満たす
　したがって，$5$ の方に『＝はつく』

　

　$6$ の方に『＝がつくかどうか』を考える
　➡ $6$ の上に $a+1$ を置いてみる

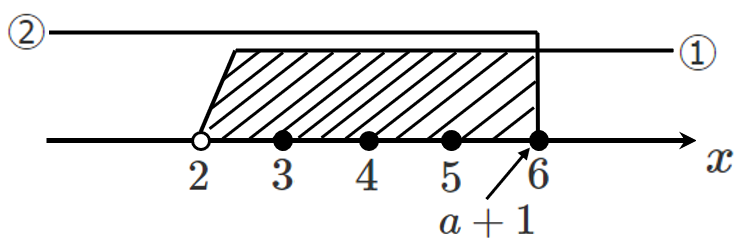
　$a+1$ の上は含むので，$6$ は共通範囲には含まれる
　すなわち，共通範囲には『 $3，4，5，6$ 』の $4$ 個になるため条件を満たさない
　したがって，$6$ の方に『＝はつかない』

　以上より，

$5$$≦$$a+1$$<$$6$

$4≦a<5$（答）

1. それぞれの不等式を解く
2. $a$ を含む値がどこの間にくればいいか考える
3. 両端でも成り立つかどうかを調べる
4. 2，3から不等式を作って解く

🔴文字係数の１次不等式を場合分けして解く方法を解説
🔴場合分けが必要な絶対値の方程式と不等式の解法を解説